初中数学浙教版九年级下册2.2 切线长定理 同步练习
试卷更新日期：2021-01-28 类型：同步测试
一、单选题
-
1. 如图，P为圆O外一点， 分别切圆O于 两点，若 ，则 （ ）.
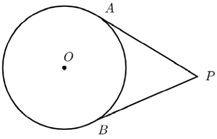A、2 B、3 C、4 D、52. 如图，PA、PB是⊙O的切线，A、B为切点，若∠P＝50°，则∠PAB的度数为（ ）
A、50° B、60° C、65° D、70°3. 如图，AB是⊙O的直径，点P在BA的延长线上，PA＝AO，PD与⊙O相切于点D，BC⊥AB交PD的延长线于点C，若⊙O的半径为1，则BC的长是（ ）
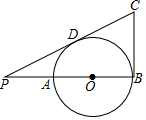A、1.5 B、2 C、 D、4.如图，AB是⊙O的弦，AO的延长线交过点B的⊙O的切线于点C，如果∠ABO=20°，则∠C的度数是（ ）
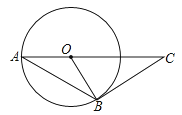A、70° B、50° C、45° D、20°5. 如图，AB，BC，CD，DA都是⊙O的切线，已知AD＝2，BC＝5，则AB＋CD的值是（ ）
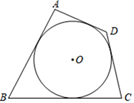A、14 B、12 C、9 D、76. 如图， 、 、 是 的切线， 、 、 是切点， 分别交 、 于 、 两点.如 ，则 的度数为（ ）
A、50° B、60° C、70° D、75°7. 如图，是用一把直尺、含60°角的直角三角板和光盘摆放而成，点 为60°角与直尺交点，点 为光盘与直尺唯一交点，若 ，则光盘的直径是（ ）．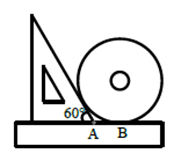
A、 B、 C、6 D、38. 如图，等边三角形ABC的边长为8，以BC上一点O为圆心的圆分别与边AB，AC相切，则⊙O的半径为（ ）
A、2 B、3 C、4 D、4-9. 如图，在矩形ABCD中，AB=4，以AB为直径在矩形内作半圆，DF切该半圆于点E，点F在边BC上．设BF=x，y=tan∠CDF，则（ ）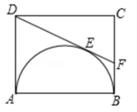
A、x2+4xy=4 B、x²-4xy=4 C、xy=4 D、xy+x²=4二、填空题
-
10. 如图，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA＝6，则△PCD的周长为.
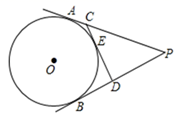11. 如图，AB、AC、BD是⊙O的切线，P、C、D为切点，如果AB＝5，AC＝3，则BD的长为 ．
12. 如图，⊙O切△ABC的BC于D，切AB、AC的延长线于E、F，△ABC的周长为18，则AE＝.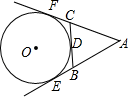
13. 如图， ， 是 的切线， ， 为切点， 是 的直径， ，则 的度数为.
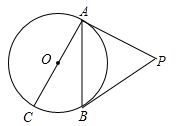14. 如图，PA、PB是⊙O的切线，若∠APO＝25°，则∠BPA＝ ．
15. 如图，在□ABCD中，AB＝5，AD＝6，AD、AB、BC分别与⊙O相切于E、F、G三点，过点C作⊙O的切线交AD于点N，切点为M．当CN⊥AD时，⊙O的半径为 ．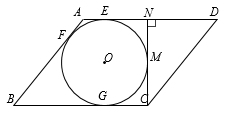
16. 如图，PA、PB是 的切线，A、B为切点，点C、D在⊙O上.若∠P＝102°，则∠A＋∠C＝°.
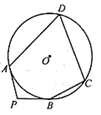17. 如图，将正方形 绕点 按逆时针方向旋转30°得到正方形 ，已知 交 于点 ， ，则四边形 的内切圆半径为 ．
三、综合题
-
18. 如图，AB是⊙O的直径，PA ， PC分别与⊙O相切于点A ， 点C ， 若∠P=60°，PA= ，求AB的长．
19. 如图， 是 的直径， 切 于点 ，点 是 上的一点，且 ， .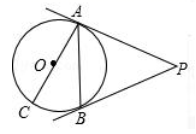
(1)、求证： 是 的切线；(2)、若 的半径为2，求弦 及 ， 的长.20. 如图，在菱形ABCD中，∠A=60°，经过点C且半径为2的⊙O分别切AB，AD于点B，D。
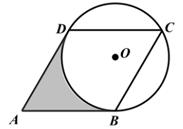(1)、求 的度数。(2)、求图中阴影部分的面积。
21. 如图，直线AB、BC、CD分别与⊙O相切于E、F、G，且AB∥CD，OB=6cm，OC=8cm．求：
(1)、∠BOC的度数；(2)、BE+CG的长；(3)、⊙O的半径．
