初中数学浙教版九年级下册 2.1 直线和圆的位置关系 同步练习
试卷更新日期:2021-01-28 类型:同步测试
一、单选题
-
1. 已知 的半径是 ,圆心 到同一平面内直线 的距离为 ,则直线 与 的位置关系是( )A、相交 B、相切 C、相离 D、无法判断2. 如图,AB是⊙O的切线,A为切点,连接OA,OB.若∠B=35°,则∠AOB的度数为( )
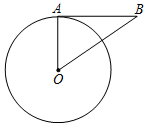 A、65° B、55° C、45° D、35°3. 如图所示,AE切⊙D于点E,AC=CD=DB=10,则线段AE的长为( )
A、65° B、55° C、45° D、35°3. 如图所示,AE切⊙D于点E,AC=CD=DB=10,则线段AE的长为( )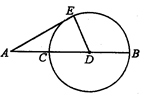 A、10 B、15 C、10 D、204. 在直角坐标平面内,已知点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,那么r的取值范围为( )A、 B、 C、 D、5. 如图,AB是半圆O的直径,点C在半圆上(不与A,B重合), 于点D,交BC于点F,下列条件中能判别CE是切线的是( )
A、10 B、15 C、10 D、204. 在直角坐标平面内,已知点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,那么r的取值范围为( )A、 B、 C、 D、5. 如图,AB是半圆O的直径,点C在半圆上(不与A,B重合), 于点D,交BC于点F,下列条件中能判别CE是切线的是( )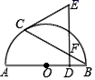 A、 B、 C、 D、6. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )
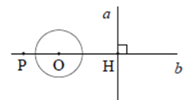
A、 B、 C、 D、6. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )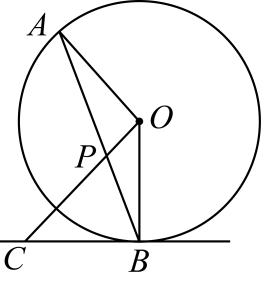 A、 B、 C、 D、7. 如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,以O为圆心1cm为半径作圆,当O从点P出发以2 cm/s速度向右作匀速运动,经过t s与直线a相切,则t为( )
A、 B、 C、 D、7. 如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,以O为圆心1cm为半径作圆,当O从点P出发以2 cm/s速度向右作匀速运动,经过t s与直线a相切,则t为( )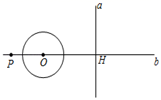 A、2s B、 s或2s C、2s或 s D、 s或 s8. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=2,tan∠OAB=
A、2s B、 s或2s C、2s或 s D、 s或 s8. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=2,tan∠OAB=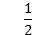 ,则AB的长是( )
,则AB的长是( ) 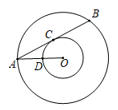 A、4 B、 C、8 D、
A、4 B、 C、8 D、二、填空题
-
9. 已知在Rt△ABC中,∠C=90º,AC=3,BC=4,⊙C与斜边AB相切,那么⊙C的半径为.10. 如果我们把太阳看作一个圆,把地平线看作一条直线,太阳在升起离开地平线后,太阳和地平线的位置关系是 .11. 如图,直线 a⊥b ,垂足为H,点P在直线b上, ,O为直线b上一动点,若以 为半径的 与直线a相切,则 的长为.
 12. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在弧BC上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=度.
12. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在弧BC上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=度.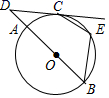 13. 已知Rt△ABC中, , , ,如果以点 为圆心的圆与斜边 有唯一的公共点,那么 的半径 的取值范围为.14. 已知Rt△ABC中,AC=3,BC=4,以C为圆心,以r为半径作圆.若此圆与线段AB只有一个交点,则r的取值范围为.
13. 已知Rt△ABC中, , , ,如果以点 为圆心的圆与斜边 有唯一的公共点,那么 的半径 的取值范围为.14. 已知Rt△ABC中,AC=3,BC=4,以C为圆心,以r为半径作圆.若此圆与线段AB只有一个交点,则r的取值范围为.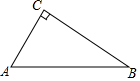 15. 如图,半圆的圆心与坐标原点重合,半圆的半径1,直线 的解析式为 若直线 与半圆只有一个交点,则t的取值范围是 .
15. 如图,半圆的圆心与坐标原点重合,半圆的半径1,直线 的解析式为 若直线 与半圆只有一个交点,则t的取值范围是 .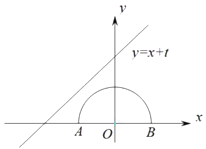 16. 如图,在Rt△ABC中,∠BCA=90°,∠A=30°,AB=4 .若动点D在线段AC上(不与点A,C重合),过点D作DE上AC交AB边于点E若点A关于点D的对称点为点F,以FC为半径作⊙C,当DE= 时,⊙C与直线AB相切.
16. 如图,在Rt△ABC中,∠BCA=90°,∠A=30°,AB=4 .若动点D在线段AC上(不与点A,C重合),过点D作DE上AC交AB边于点E若点A关于点D的对称点为点F,以FC为半径作⊙C,当DE= 时,⊙C与直线AB相切.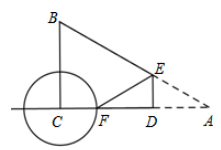
三、综合题
-
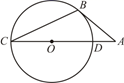
17. 如图,AB与⊙O相切于点B,AO及AO的延长线分别交⊙O于D、C两点,若∠A=40°,求∠C的度数.
 18. 已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AD为弦作⊙O,使圆心O在AB上.
18. 已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AD为弦作⊙O,使圆心O在AB上.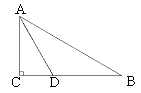 (1)、用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹) ;(2)、求证:BC为⊙O的切线.19. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
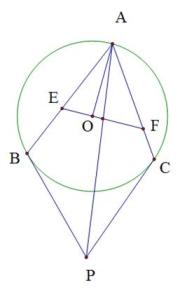
(1)、用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹) ;(2)、求证:BC为⊙O的切线.19. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.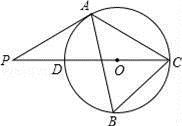 (1)、求证:PA是⊙O的切线;(2)、若PD=1,求⊙O的直径.20. 如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且 ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
(1)、求证:PA是⊙O的切线;(2)、若PD=1,求⊙O的直径.20. 如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且 ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.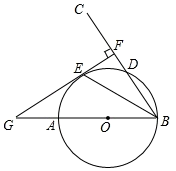 (1)、证明:GF是⊙O的切线;(2)、若AG=6,GE=6 ,求⊙O的半径.
(1)、证明:GF是⊙O的切线;(2)、若AG=6,GE=6 ,求⊙O的半径.