2016年浙江省杭州市五校联盟高考数学一诊试卷(文科)
试卷更新日期:2016-07-12 类型:高考模拟
一、单选题
-
1. 下列命题中,真命题是( )A、存在x<0,使得2x>1 B、对任意x∈R,x2﹣x+1>0 C、“x>1”是“x>2”的充分不必要条件 D、“P或q是假命题”是“非p为真命题”的必要而不充分条件2. 定义在R上的奇函数f(x)满足f(x+1)=f(﹣x),当x∈(0,1)时,f(x)= , 则f(x)在区间(1,)内是( )
A、增函数且f(x)>0 B、增函数且f(x)<0 C、减函数且f(x)>0 D、减函数且f(x)<03. 若函数f(x)=x2+ex﹣(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )A、(﹣) B、() C、() D、()4. 在同一个坐标系中画出函数y=ax , y=sinax的部分图象,其中a>0且a≠1,则下列所给图象中可能正确的是( )A、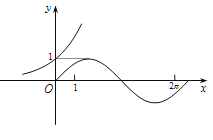 B、
B、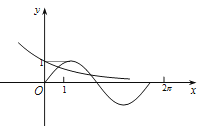 C、
C、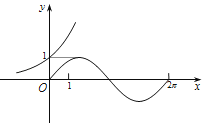 D、
D、 5. 已知倾斜角为θ的直线,与直线x﹣3y+l=0垂直,则=( )A、 B、- C、 D、-6. 已知三个向量= , = , =共线,其中a、b、c、A、B、C分别是△ABC的三条边及相对三个角,则△ABC的形状是( )
5. 已知倾斜角为θ的直线,与直线x﹣3y+l=0垂直,则=( )A、 B、- C、 D、-6. 已知三个向量= , = , =共线,其中a、b、c、A、B、C分别是△ABC的三条边及相对三个角,则△ABC的形状是( )
A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形7. 某几何体的三视图如图所示,则该几何体的体积为( ) A、 B、 C、 D、8. 下列三图中的多边形均为正多边形,M,N是所在边的中点,双曲线均以图中的F1 , F2为焦点,设图示①②③中的双曲线的离心率分别为e1 , e2 , e3、则e1 , e2 , e3的大小关系为( )
A、 B、 C、 D、8. 下列三图中的多边形均为正多边形,M,N是所在边的中点,双曲线均以图中的F1 , F2为焦点,设图示①②③中的双曲线的离心率分别为e1 , e2 , e3、则e1 , e2 , e3的大小关系为( ) A、e1>e2>e3 B、e1<e2<e3 C、e2=e3<e1 D、e1=e3>e2
A、e1>e2>e3 B、e1<e2<e3 C、e2=e3<e1 D、e1=e3>e2二、填空题
-
9. 设平面点集A={(x,y)|(x﹣1)2+(y﹣1)2≤1},B={(x,y)|(x+1)2+(y+1)2≤1},C={(x,y)|y﹣≥0},则(A∪B)∩C所表示的平面图形的面积是10. 已知函数f(x)= , 则f(6)=11. 已知等差数列{an}中,满足S3=S10 , 且a1>0,Sn是其前n项和,若Sn取得最大值,则n=12. 下列四种说法
①在△ABC中,若∠A>∠B,则sinA>sinB;
②等差数列{an}中,a1 , a3 , a4成等比数列,则公比为;
③已知a>0,b>0,a+b=1,则+的最小值为5+2;
④在△ABC中,已知== , 则∠A=60°.
正确的序号有
13. 实数x、y满足 , 则z=x2+y2+2x﹣2y的最小值为14. 一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积V= 15. 已知椭圆的半焦距为C,(C>0),左焦点为F,右顶点为A,抛物线y2=(a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率是
15. 已知椭圆的半焦距为C,(C>0),左焦点为F,右顶点为A,抛物线y2=(a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率是三、解答题
-
16. 在△ABC中,角A,B,C的对边分别为a,b,c,且满足bcosA=(2c+a)cos(π﹣B)
(1)求角B的大小;
(2)若b=4,△ABC的面积为 , 求a+c的值.
17. 如图,边长为的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=AB=1,点M在线段EC上.(Ⅰ)证明:平面BDM⊥平面ADEF;
(Ⅱ)判断点M的位置,使得三棱锥B﹣CDM的体积为 .
 18. 已知值域为[﹣1,+∞)的二次函数满足f(﹣1+x)=f(﹣1﹣x),且方程f(x)=0的两个实根x1 , x2满足|x1﹣x2|=2.
18. 已知值域为[﹣1,+∞)的二次函数满足f(﹣1+x)=f(﹣1﹣x),且方程f(x)=0的两个实根x1 , x2满足|x1﹣x2|=2.(1)求f(x)的表达式;
(2)函数g(x)=f(x)﹣kx在区间[﹣1,2]内的最大值为f(2),最小值为f(﹣1),求实数k的取值范围.
