湖北省孝感市云梦县2021届九年级上学期数学12月月考试卷
试卷更新日期:2021-01-27 类型:月考试卷
一、单选题
-
1. 下列图形中既是轴对称图形,又是中心对称图形的是( )A、
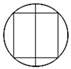 B、
B、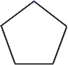 C、
C、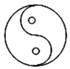 D、
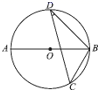
D、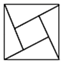 2. 方程 的解是( )A、 B、 C、 , D、无解3. 平面直角坐标系内,点M 关于原点对称点的坐标是( )A、 B、 C、 D、4. 如右图,⊿ABC内接于⊙O,若∠OAB=28°则∠C的大小为( )
2. 方程 的解是( )A、 B、 C、 , D、无解3. 平面直角坐标系内,点M 关于原点对称点的坐标是( )A、 B、 C、 D、4. 如右图,⊿ABC内接于⊙O,若∠OAB=28°则∠C的大小为( )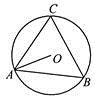 A、62° B、56° C、60° D、28°5. 对于二次函数y=﹣ (x﹣2)2﹣3,下列说法正确的是( )A、当x>2时,y随x的增大而增大 B、当x=2时,y有最大值﹣3 C、图象的顶点坐标为(﹣2,﹣3) D、图象与x轴有两个交点6. 半径为 的圆的内接正六边形的边心距是( )A、 B、 C、 D、7. 如图,将△ABC绕点A逆时针旋转80°,得到△ADE,若点D在线段BC的延长线上,则∠PDE的大小为( )
A、62° B、56° C、60° D、28°5. 对于二次函数y=﹣ (x﹣2)2﹣3,下列说法正确的是( )A、当x>2时,y随x的增大而增大 B、当x=2时,y有最大值﹣3 C、图象的顶点坐标为(﹣2,﹣3) D、图象与x轴有两个交点6. 半径为 的圆的内接正六边形的边心距是( )A、 B、 C、 D、7. 如图,将△ABC绕点A逆时针旋转80°,得到△ADE,若点D在线段BC的延长线上,则∠PDE的大小为( )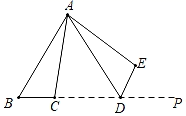 A、80° B、100° C、120° D、不能确定8. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
A、80° B、100° C、120° D、不能确定8. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )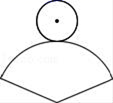 A、r B、2 r C、 r D、3r9. 如图所示,正方形 的边长为 ,点 分别为边 的中点,动点 从点 向点 运动, 到点 时停止运动;同时,动点 从点 出发,沿 运动,已知点 的运动速度相同,设点 的运动路程为 的面积为 ,则能大致表示 与 的函数关系的图象是( )
A、r B、2 r C、 r D、3r9. 如图所示,正方形 的边长为 ,点 分别为边 的中点,动点 从点 向点 运动, 到点 时停止运动;同时,动点 从点 出发,沿 运动,已知点 的运动速度相同,设点 的运动路程为 的面积为 ,则能大致表示 与 的函数关系的图象是( )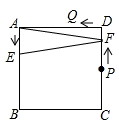 A、
A、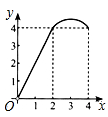 B、
B、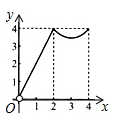 C、
C、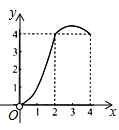 D、
D、 10. 如图,正方形 的边长为1, , 是对角线.将 绕着点 顺时针旋转45°得到 , 交 于点 ,连接 交 于点 ,连接 .则下列结论:
10. 如图,正方形 的边长为1, , 是对角线.将 绕着点 顺时针旋转45°得到 , 交 于点 ,连接 交 于点 ,连接 .则下列结论:①四边形 是菱形 ② ③ ④
其中正确的结论是有( )个
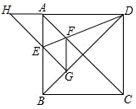 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 若关于 的方程 的一个根为1,则方程的另一个根为.12. 如图, 为 的直径, , 为 上的两点,若 , ,则 度.
 13. 如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为 .
13. 如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为 .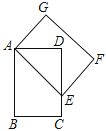 14. 某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支. 若主干、支干和小分支的总数是 57,设每个支干长出 x 个小分支,则可列方程为15. 如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2 . 将⊙P沿着与y轴平行的方向平移,使⊙P与 轴相切,则平移距离为.
14. 某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支. 若主干、支干和小分支的总数是 57,设每个支干长出 x 个小分支,则可列方程为15. 如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2 . 将⊙P沿着与y轴平行的方向平移,使⊙P与 轴相切,则平移距离为.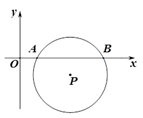 16. 如图,已知抛物线 和直线 .我们规定:当 取任意一个值时, 对应的函数值分别为 和 ,若 ,取 和 中较小值为 ;若 ,记 .①当 时, ;②当 时, 随 的增大而增大;③使得 大于4的 的值不存在;④若 ,则 .上述结论正确的是.
16. 如图,已知抛物线 和直线 .我们规定:当 取任意一个值时, 对应的函数值分别为 和 ,若 ,取 和 中较小值为 ;若 ,记 .①当 时, ;②当 时, 随 的增大而增大;③使得 大于4的 的值不存在;④若 ,则 .上述结论正确的是.
三、解答题
-
17.(1)、(2)、 .18. 如图,已知 是 的直径, 是 上的点, ,交 于点E,连结 .
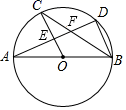 (1)、求证: ;(2)、若 ,求扇形 的面积.19. 已知△ABC在平面直角坐标系中的位置如图所示.
(1)、求证: ;(2)、若 ,求扇形 的面积.19. 已知△ABC在平面直角坐标系中的位置如图所示.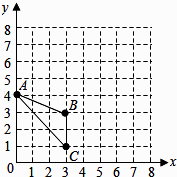 (1)、分别写出图中点A和点C的坐标;(2)、画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;(3)、求点A旋转到点A′所经过的路线长(结果保留π).20. 已知关于 的一元二次方程 有两个实数根 , .(1)、求 的取值范围;(2)、若 ,求 的值.21. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.
(1)、分别写出图中点A和点C的坐标;(2)、画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;(3)、求点A旋转到点A′所经过的路线长(结果保留π).20. 已知关于 的一元二次方程 有两个实数根 , .(1)、求 的取值范围;(2)、若 ,求 的值.21. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.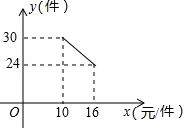 (1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?22. 如图, 是 的直径,弦 垂直半径 , 为垂足, ,连接 , ,过点 作 ,交 的延长线于点 .
(1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?22. 如图, 是 的直径,弦 垂直半径 , 为垂足, ,连接 , ,过点 作 ,交 的延长线于点 .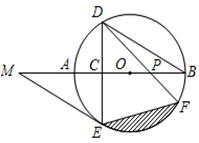 (1)、求证: 是 的切线;(2)、若弦 与直径 相交于点 ,当 时,求图中阴影部分的面积.23. 如图1,将两块全等的直角三角形纸片 和 叠放在一起,其中 , , ,顶点 与边 的中点重合.旋转 .
(1)、求证: 是 的切线;(2)、若弦 与直径 相交于点 ,当 时,求图中阴影部分的面积.23. 如图1,将两块全等的直角三角形纸片 和 叠放在一起,其中 , , ,顶点 与边 的中点重合.旋转 .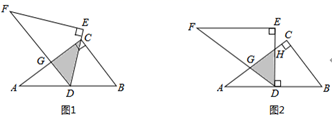 (1)、若 经过点 , 交 于点 ,求证: 为 的中点;(2)、合作交流:受问题(1)的启发,将 绕点 旋转,使 交 于点 , 交 于点 ,如图2,
(1)、若 经过点 , 交 于点 ,求证: 为 的中点;(2)、合作交流:受问题(1)的启发,将 绕点 旋转,使 交 于点 , 交 于点 ,如图2,①求证: 为 的中点;
②求 的长.
24. 已知抛物线 与 轴交于点 和点 ,与直线 交于点 和点 , 为抛物线的顶点,直线 是抛物线的对称轴.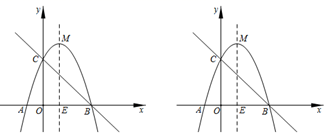 (1)、求抛物线的解析式为 , 不等式 的解集为.(2)、连接 , ,求 的面积.(3)、点 为直线 上方抛物线上一点,设 为点 到直线 的距离,当 有最大值时,求点 的坐标.
(1)、求抛物线的解析式为 , 不等式 的解集为.(2)、连接 , ,求 的面积.(3)、点 为直线 上方抛物线上一点,设 为点 到直线 的距离,当 有最大值时,求点 的坐标.