河南省洛阳市洛宁县2021届九年级上学期数学第三次月考试卷

试卷更新日期：2021-01-27 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $\sqrt{12} = 4 \sqrt{3}$ B、 $5 \sqrt{2} - 3 \sqrt{2} = 2$ C、2cos 60°= $\sqrt{3}$ D、 $\sqrt{8} \times \frac{1}{\sqrt{2}} - 2 = 0$

查看试题解析
2. 下列事件中为必然事件的是（）

A、如果 $a^{2} = b^{2}$ ，那么a=b B、两边及其一角对应相等的两个三角形全等 C、射击运动员射击一次，命中10环 D、长度分别是4， 6，9的三条线段能围成一个三角形

查看试题解析
3. 关于x的一元二次方程 $x^{2}$ $+ (a — 2) x — 5 + a = 0$ 根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、无法确定

查看试题解析
4. 如图，在数学兴趣小组探究活动中，小明要测量小河两岸相对的两点P，A的距离，他和同学利用工具测得PC=50米，∠PCA= $α$ ，根据上述测量数据可计算得到小河宽度PA为（）

A、 $\frac{50}{\sin α}$ 米 B、50 $\sin α$ 米 C、 $\frac{50}{\tan α}$ 米 D、50tanα米

查看试题解析
5. 对抛物线：y=-x²+2x-3而言，下列结论正确的是（　 )

A、与x轴有两个交点 B、开口向上 C、与y轴交点坐标是(0，3) D、顶点坐标是(1,-2)

查看试题解析
6. 学校教学楼前面有一根高是4.2米的旗杆，在某时刻太阳光下的影子长是6.3米，与此同时，在旗杆周边的一棵大树在地面上投影出的影子长是9米，则此大树的高度是（）

A、4.8米 B、8.4米 C、6米 D、9米

查看试题解析
7. 如图，已知在4 $\times$ 4的网格中，每个小正方形的边长都是1，△ABC的顶点都在这些小正方形的顶点上，则cos∠CAB的值为（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{3 \sqrt{5}}{5}$ D、 $\frac{4}{5}$

查看试题解析
8. 如图，E是▱ABCD的边AD上的一点，连接BE并延长，交CD的延长线于点F，若AE： BC =3： 5，则FD： DC的值为（）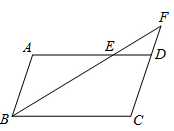

A、2 ： 3 B、2：5 C、3 ： 4 D、3 ： 5

查看试题解析
9. 将拋物线C：y= $x^{2} + 3 x - 10$ 平移到 $C^{'}$ ，若两条拋物线C， $C^{'}$ 关于直线x = 1对称，则下列平移方法中正确的是（）

A、将抛物线C向右平移1个单位 B、将抛物线C向右平移3个单位 C、将抛物线C向右平移5个单位 D、将抛物线C向右平移6个单位

查看试题解析
10. 如图，在正方形ABCD中.以AD、AB为斜边分别向外和向内作Rt△ADN和Rt△ABM，且满足AN=AM，连接MN交AD于点T.若DC=4，tan∠ABM= $\frac{1}{3}$ ，则AT的长为（）

A、1 B、 $\frac{4}{3}$ C、 $\frac{5}{4}$ D、 $\frac{3}{2}$

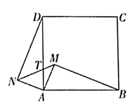查看试题解析

二、填空题

11. 计算： ${(1 - 2 \sqrt{3})}^{2}$ =

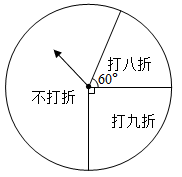
查看试题解析
12. 某商场的打折活动规定：凡在本商场购物，结账时可转动一次如图所示的转盘（转到公共线位置时重转），并根据所转结果打折或不打折，某顾客在结账时转动一次该转盘，其结果是不打折的概率为

查看试题解析
13. 一个函数有下列性质：①它的图象不经过第四象限；②图象经过点（1，2）；③当x>1时，函数值y随自变量x的增大而增大.满足上述三条性质的二次函数解析式可以是（只要求写出一个）.

查看试题解析
14. 某市有一块正方形的空地需要美化，规划设计图如图所示，空地正中间修建一个圆形喷泉，在四个角分别修建四个四分之一圆形的水池，其余部分种植花草.若喷泉和水池的半径都相同，喷泉边缘到空地边界的距离都为3 m，种植花草的区域的面积为60 m² ，设水池半径为 $x$ m，根据题意可列出方程为

查看试题解析
15. 如图，在 Rt△ABC 中，∠ACB = 90°，AC= 3，sin A = $\frac{4}{5}$ ，若 E 为边 BC 的中点，则点E到Rt△ABC的中线CD的距离EF为.

查看试题解析

三、解答题

16. 解方程： ${(x - 1)}^{2} - 2 (x - 1) = - 1$ .

查看试题解析
17. 如图，已知A（－4，2），B（－2，6），C（0，4）是直角坐标系平面上三点.

（ 1 ）把△ABC向右平移4个单位再向下平移1个单位，得到△A₁B₁C₁ ，画出平移后的图形；

（ 2 ）若△ABC内部有一点P（a，b），则平移后它的对应点P₁的坐标为；

（ 3 ）以原点O为位似中心，将△ABC缩小为原来的一半，得到△A₂B₂C₂ ，请在所给的坐标系中作出所有满足条件的图形.

查看试题解析
18. 下表所示的是数学兴趣小组填写的数学实践活动报告的部分内容.

已知四边形ABCD为矩形，DG丄EF于点G，且点A、B、C、D、E、F、G都在同一竖直平面内，求铁塔FE的高度.（结果精确到1米；参考数据：sin 44° $\approx$ 0.69，cos 44° $\approx$ 0.72， tan 44° $\approx$ 0.97）

查看试题解析
19. 某校团委在“五·四”青年节举办了一次“我的中国梦”作文大赛，广三批对全校20个班的作品进行评比在第一批评比中，随机抽取A、B、C、D四个班的征集作品，对其数量进行统计后，绘制如下两幅不完整的统计图，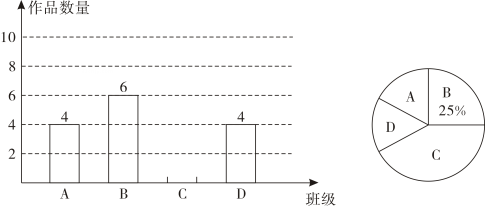

(1)、第一批所抽取的4个班共征集到作品件；在扇形统计图中表示C班的扇形的圆心角的度数为；

(2)、补全条形统计图；

(3)、第一批评比中，A班D班各有一件、B班C班各有两件作品获得一等奖．现要在获得一等奖的作品中随机抽取两件在全校展出，用树状图或列表法求抽取的作品在两个不同班级的概率．

查看试题解析
20. 阅读以下材料，并按要求完成相应的任务.
构建几何图形解决代数问题是“数形结合”思想的重要应用，例如在计算tan 15°时，可构造如图所示的图形.在 Rt△ACB 中，∠C= 90°， ∠ABC=30°， AC=x（x>0），延长 CB 至点 D，使得 BD=AB，连接AD，易知∠D =15°，CD=BD+BC=AB+BC= $2 x + \sqrt{3} x$ ，所以tan15°=tanD……

任务：

(1)、请根据上面的步骤，完成tan 15°的计算.

(2)、类比这种方法，画出图形，并计算tan22.5°的值.

查看试题解析

21. 某公司销售一种进价为20元/个的计算器，其销售量y（万个）与销售价格x（元/个）的变化如下表：

价格：x（元/个）	…	30	40	50	60	…
销售量y（万个）	…	5	4	3	2

同时，销售过程中的其他开支（不含进价）总计40万元.

(1)、观察并分析表中的y与x之间的对应关系，用学过的一次函数、反比例函数或二次函数的之间有关知识求y（万个）与x（元/个）之间的函数解析式.

(2)、求该公司销售这种计算器的净得利润z（万元）与销售价格x（元/个）之间的函数解析式，销售价格定为多少元时净得利润最大，最大值是多少？

查看试题解析

22. 如图，二次函数： $y_{1}$ = ${ax}^{2}$ + $bx + c (a \neq 0$ ）的图象与一次函数： $y_{2}$ = $x + d$ 的图象交于A（0，1），B两点，C（1，0）为二次函数图象的顶点.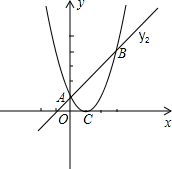

(1)、求二次函数： $y_{1}$ = ${ax}^{2}$ + $bx + c (a \neq 0$ ）的解析式.

(2)、定义函数 $f$ 当自变量 $x$ 任取一值时， $x$ 对应的函数值分别为 $y_{1}$ 或 $y_{2}$ ，若 $y_{1} \neq y_{2}$ ，函数 $f$ 的函数值等于 $y_{1}$ 、 $y_{2}$ 中的较小值；若 $y_{1} = y_{2}$ ，函数 $f$ 的函数值等于 $y_{1} （$ 或 $y_{2} ）$ .当直线 $y_{3} = kx$ - $\frac{1}{2} （ k$ >0）与函数 $f$ 的图象只有两个交点时，求 $k$ 的值.

查看试题解析
23. 如图，在矩形ABCD中， $\frac{BC}{AB}$ ＝ $\frac{1}{2}$ ，F、G分别为边AB、DC上的动点，连接GF，将四边形AFGD沿GP折叠，使点A落在边BC上的点E处，得到四边形EFGP，EP交CD于点H，连接AE交GF于点O.

(1)、求GF与AE之间的位置关系.

(2)、求 $\frac{GF}{AE}$ 的值.

(3)、连接CP，若tan∠CGP＝ $\frac{3}{4}$ ，GF＝2 $\sqrt{10}$ ，请直接写出CP的长.

查看试题解析