湖北省武汉市江汉区四校2020-2021学年七年级上学期数学12月联考试卷

试卷更新日期：2021-01-26 类型：月考试卷

进入出卷网下载

一、单选题

1. 在0，1，-1，2这四个数中，是负数的是（）

A、0 B、1 C、-1 D、2

查看试题解析
2. 化简 ${(- 1)}^{2020}$ 的值是（）

A、1 B、 $- 2020$ C、2020 D、 $- 1$

查看试题解析
3. 下列运用等式的性质对等式进行变形，正确的是（）

A、由 $\frac{x}{5} = 0$ 得 $x = 5$ B、由 $x + 2 = 8$ 得 $x = 10$ C、由 $- 3 x = 12$ 得 $x = 4$ D、由 $6 x = 9 x + 5$ 得 $- 3 x = 5$

查看试题解析
4. 下列说法中，正确的是（）

A、 $\frac{1}{3}$ πx²的系数是 $\frac{1}{3}$ B、x⁴+x³y²－1 是四次三项式 C、－3x²的系数为－3 D、 $3^{2} x^{3} y$ 的次数是 6

查看试题解析
5. 下列近似数的结论不正确的是（）

A、0.1 （精确到0.1） B、0.05 （精确到百分位） C、0.50 （精确到百分位） D、0.100 （精确到0.1）

查看试题解析
6. 若关于 $x$ 的方程 $3 x - m = x + 2$ 的解是 $x = - 2$ ，则 $m$ 的值等于（）

A、6 B、0 C、2 D、 $- 6$

查看试题解析
7. 把方程 $\frac{x - 1}{0.6} + \frac{0.5 x + 8}{0.9} = 12$ 的分母化为整数，结果应为（）

A、 $\frac{x - 1}{6} + \frac{5 x + 8}{9} = 12$ B、 $\frac{10 x - 10}{6} + \frac{5 x + 80}{9} = 12$ C、 $\frac{10 x - 10}{6} + \frac{5 x + 80}{9} = 120$ D、 $\frac{x - 1}{6} + \frac{5 x + 8}{9} = 120$

查看试题解析
8. 当 $x = 4$ 时，多项式 $a x^{3} + b x + 1$ 的值为6，则当 $x = - 4$ 时， $a x^{3} + b x + 1$ 的值为（）

A、 $- 6$ B、 $- 7$ C、 $- 4$ D、 $- 5$

查看试题解析
9. 某水库建设工地调来60人参加挖土和运土，已知4人挖出的土1人恰好能全部运走，怎样调配劳动力才能使挖出来的土能及时运走？解决此问题，可设安排 $x$ 人挖土，其他人运土，则下列方程错误的是（）

A、 $x + \frac{1}{4} x = 60$ B、 $x = 4 (60 - x)$ C、 $x + 4 x = 60$ D、 $60 - x = \frac{1}{4} x$

查看试题解析

10. 某电视台组织知识竞赛，共设20道选择题，各题分值相同，每题必答.下表记录了5个参赛者的得分情况

参赛者	答对题数	答错题数	得分
$A$	20	0	100
$B$	18	2	88
$C$	14	6	64
$D$	15	5	70
$E$	9	11	34

下列说法有误的是（）

A、胜一场积5分，负一场扣1分 B、某参赛选手得了80分 C、某参赛选手得了76分 D、某参赛选手得分可能为负数

查看试题解析

二、填空题

11. 光的速度大约是300000千米/秒，将300000用科学记数法表示为．

查看试题解析
12. 单项式 $2 a^{x - 2} b^{3}$ 与 $\frac{1}{3} a^{6 - x} b^{3}$ 是同类项，则 $x =$ .

查看试题解析
13. 若 $(| m | - 1) x^{2} + (m - 1) x - 4 = 0$ 是关于 $x$ 的一元一次方程，则 $m$ 的值是.

查看试题解析
14. 某轮船顺水航行 3h，逆水航行 1.5h，已知轮船在静水中的速度为 a km/h，水流速度是 y km/h，则轮船共航行km.

查看试题解析
15. 现对某商品降价20%促销，为了使总金额不变，销售量要比按原价销售时增加.

查看试题解析
16. 将全体正偶数排成一个三角形数阵：按照以上规律排列，第25行第20个数是.
2

4   6

8   10   12

14   16   18   20

22   24   26   28   30

……

查看试题解析

三、解答题

17. 计算：

(1)、 $12 - (- 18) + (- 7) - 15$

(2)、 $6 \times (- 2^{2}) + (\frac{7}{12} - \frac{3}{4} - \frac{5}{9}) \times 36$

查看试题解析
18.

(1)、求 $\frac{1}{2} x - 2 (x - \frac{1}{3} y^{2}) + (- \frac{3}{2} x + \frac{1}{3} y^{2})$ 的值，其中 $x = - 2, y = \frac{2}{3}$ .

(2)、已知 $| a | = 5, | b | = 4$ ，且 $| a + b | = | a | + | b |$ .求 $- 6 a b + a b + 8 (a b - 1)$ 的值.

查看试题解析
19. 解方程：

(1)、 $2 - (4 - x) = 6 x - 2 (x + 1)$

(2)、 $\frac{x + 1}{4} - 1 = \frac{2 x - 1}{6}$

查看试题解析
20. 在抗洪抢险中，解放军战士的冲锋舟加满油，沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B地，约定向东为正方向，当天的航行路程记录如下(单位：千米)：+14，−9，+8，−7，+13，−6，+12，−5．

(1)、请你帮忙确定B地位于A地的什么方向，距离A地多少千米?

(2)、救灾过程中，冲锋舟离出发点A最远处千米；

(3)、若冲锋舟每千米耗油0.5升，油箱容量为28升，求冲锋舟当天救灾过程中至少还需补充多少升油?

查看试题解析
21. 先化简再求值， $A = 2 x^{2} - \frac{1}{2} x + 3, B = x^{2} + m x + \frac{1}{2}$

(1)、当 $m = - 1$ ，求 $5 (A - B) - 3 (- 2 B + A)$

(2)、若 $A - 2 B$ 的值与 $x$ 无关，求 $m^{2} - [- 2 m^{2} - (2 m + 6) - 3 m]$

查看试题解析

22. 为加强公民节水意识，合理利用水资源某市采用价格调控手段达到节水目的，该市自来水收费的价目表如下（水费按月计算用水量的单位

m^{3}

立方米）

价目表
每月用水量（单位 $m^{3}$ 立方米）	价格
不超过 ${10m}^{3}$ 的部分	2元/ $m^{3}$
超过 ${10m}^{3}$ 但不超过 ${18m}^{3}$ 的部分	3元/ $m^{3}$
超过 ${18m}^{3}$ 的部分	6元/ $m^{3}$

(1)、若小明家1月和2月的用水量分别为

{6m}^{3}

和

{15m}^{3}

，则应收水费分别为元和元.

(2)、若小明家3月的用水量为a

m^{3}

，且

a > 18

求应收水费多少元（用含

a

的式子表示）

(3)、若小明家4月和5月共用水

40 m^{3}

，4月份用水量低于5月份的用水量，且4，5两个月共交水费118元，求4月、5月用水量分别为多少

m^{3}

？

查看试题解析

23. 已知 $A 、 B 、 C$ 三点在数轴上的位置如图所示，它们表示的数分别是 $a 、 b 、 c$ .

(1)、填空： $a b c$ 0， $a + b$ $a c ， a b - a c$ 0；（填“>”，“=”或“<”）

(2)、若 $| a | = 2$ ，点 $B$ 到点 $A 、 C$ 的距离相等，求 $b 、 c$ 之间的数量关系；

(3)、若 $M$ 是数轴上 $B ， C$ 两点之间的一个动点设点 $M$ 表示的数为 $m$ .当 $M$ 点在运动过程中， $\frac{b}{2} = \frac{m}{5} = \frac{c}{7}$ ，且 $b m - m c + b c = - 99$ ，求， ${(3 b - 4 m + 2 c)}^{2} + \frac{1}{7} b cm$ 的值.

查看试题解析
24. 已知有理数 $a ， b ， c$ 在数轴上所对应的点分别是 $A ， B ， C$ 三点，且 $a ， b$ 满足：①多项式 $- \frac{1}{2} x^{| a |} + (a - 2) x + 7$ 是关于 $x$ 的二次三项式：② ${(b - 1)}^{2} + | c - 5 | = 0$

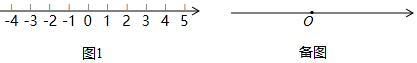(1)、请在图1的数轴上描出 $A ， B ， C$ 三点，并直接写出 $a ， b ， c$ 三数之间的大小关系(用“<”连接) ；

(2)、点 $P$ 为数轴上 $C$ 点右侧一点，且点 $P$ 到 $A$ 点的距离是到 $C$ 点距离的2倍，求点 $P$ 在数轴上所对应的有理数；

(3)、点 $A$ 在数轴上以每秒1个单位长度的速度向左运动，同时点 $B$ 和点 $C$ 在数轴上分别以每秒 $m$ 个单位长度和4个单位长度的速度向右运动(其中 $m < 4$ )，若在整个运动的过程中，点 $B$ 到点 $A$ 的距离与点 $B$ 到点 $C$ 的距离差始终不变，求 $m$ 的值.

查看试题解析