浙江省锦绣育才教育集团2020-2021学年八年级上学期数学12月月考试卷
试卷更新日期:2021-01-26 类型:月考试卷
一、单选题
-
1. 已知线段 a=2cm,b=4cm,则下列长度的线段中,能与 a,b组成三角形的是( )A、2cm B、4cm C、6cm D、8cm2. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、3. 如图,若△ABC与△DEF关于直线l对称,BE交l于点O , 则下列说法不一定正确的是( )
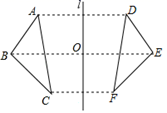 A、AB∥EF B、AC=DF C、AD⊥l D、BO=EO4. 若x+a<y+a,ax>ay,则( )
A、AB∥EF B、AC=DF C、AD⊥l D、BO=EO4. 若x+a<y+a,ax>ay,则( )
A、x>y,a>0 B、x>y,a<0 C、x<y,a>0 D、x<y,a<05. 对函数 的描述错误是( )A、y随x的增大而减小 B、图象经过第一、三、四象限 C、图象与x轴的交点坐标为 D、图象与坐标轴交点的连线段长度等于6. 如图,在平面直角坐标系中, 平行于 轴,点 坐标为 , 在 点的左侧, ,若 点在第二象限,则 的取值范围是( )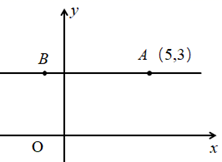 A、 B、 C、 D、7. 等腰三角形的周长12,腰长为 ,底边长为 ,则 与 的函数关系式对应图象是( )A、
A、 B、 C、 D、7. 等腰三角形的周长12,腰长为 ,底边长为 ,则 与 的函数关系式对应图象是( )A、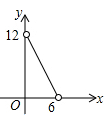 B、
B、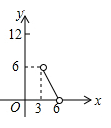 C、
C、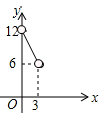 D、
D、 8. 如图,在 中, ,D、E是 内两点, 平分 , ,若 , ,则 的长度是( )
8. 如图,在 中, ,D、E是 内两点, 平分 , ,若 , ,则 的长度是( )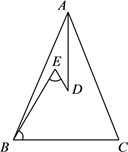 A、12 B、11 C、10 D、99. 若不等式组 的解是x>﹣1,则m的值是( )A、﹣1 B、﹣3 C、﹣1或﹣3 D、﹣1<m<110. 如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )
A、12 B、11 C、10 D、99. 若不等式组 的解是x>﹣1,则m的值是( )A、﹣1 B、﹣3 C、﹣1或﹣3 D、﹣1<m<110. 如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )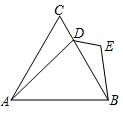 A、(m﹣60)° B、(180﹣2m)° C、(2m﹣90)° D、(120﹣m)°
A、(m﹣60)° B、(180﹣2m)° C、(2m﹣90)° D、(120﹣m)°二、填空题
-
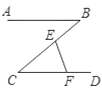
11. 函数 的自变量x的取值范围是.12. 如图,折线A-B-C-D构成的“Z”型图中,AB∥CD,E,F分别是BC,CD上的点,若∠B=40°,∠CEF=70°,则∠EFD等于
 13. 一个小球由地面沿着坡比1:2的坡面向上前进了5米,此时小球距离地面的高度为米.14. 如图,已知AB⊥CD,△ABD,△BCE都是等腰直角三角形,如果CD=8,BE=3,则AC等于.
13. 一个小球由地面沿着坡比1:2的坡面向上前进了5米,此时小球距离地面的高度为米.14. 如图,已知AB⊥CD,△ABD,△BCE都是等腰直角三角形,如果CD=8,BE=3,则AC等于. 15. 等腰三角形的一腰上的高与另一腰所在直线的夹角为40°,则这个三角形的底角为 .16. 某学校创客小组进行机器人跑步大赛,机器人小 和小 从同一地点同时出发,小 在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有(填序号).
15. 等腰三角形的一腰上的高与另一腰所在直线的夹角为40°,则这个三角形的底角为 .16. 某学校创客小组进行机器人跑步大赛,机器人小 和小 从同一地点同时出发,小 在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有(填序号).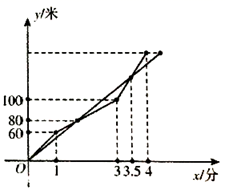
①两个机器人第一次相遇时间是在第2分钟;
②小 每分钟跑50米;
③赛程总长200米;
④小 到达终点的时候小 距离终点还有20米.
三、解答题
-
17. 计算:(1)、解不等式组(2)、化简18. 已知 , ,求下列代数式的值.(1)、(2)、19. 已知:在平面直角坐标系 中, 如图所示.
 (1)、在y轴上找一点P,使得 的面积为 面积的一半,求点P的坐标.(2)、将 进行平移,使得点A平移到点O,作出平移后的 ,并求出平移的距离.20. 为响应市政府“创建国家森林城市”的号召,某小区计划购进A,B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元。设购进A种树苗x棵,购买两种树苗的总费用为w元。(1)、写出w(元)关于x(棵)的函数关系式;(2)、若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用。21. 如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
(1)、在y轴上找一点P,使得 的面积为 面积的一半,求点P的坐标.(2)、将 进行平移,使得点A平移到点O,作出平移后的 ,并求出平移的距离.20. 为响应市政府“创建国家森林城市”的号召,某小区计划购进A,B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元。设购进A种树苗x棵,购买两种树苗的总费用为w元。(1)、写出w(元)关于x(棵)的函数关系式;(2)、若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用。21. 如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.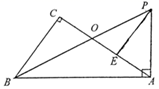 (1)、求证:AP=AO;(2)、求证:PE⊥AO.
(1)、求证:AP=AO;(2)、求证:PE⊥AO.
