陕西省西安市未央区西航二中2020-2021学年八年级上学期数学第二次月考试卷
试卷更新日期:2021-01-26 类型:月考试卷
一、单选题
-
1. 下列方程组中是二元一次方程组的是( )A、 B、 C、 D、2. 数据8,6,5,4,5的众数是( )A、8 B、6 C、5 D、43. 已知 是一次函数 图象上的两点,则 与 的大小关系是( )A、 B、 C、 D、以上都不对4. 已知2x﹣3y=1,用含x的代数式表示y正确的是( )A、y= x﹣1 B、x= C、y= D、y=﹣ ﹣ x5. 如图所示的是一种机器人行走的路径,机器人从 处先往东走 ,又往北走 ,遇到障碍后又往西走 ,再转向北走 后往东一拐仅走 就到达了 .则点 与点 之间的直线距离是( )
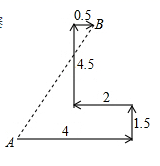 A、 B、 C、 D、6. 已知 ,则 的立方根为( )A、1 B、 C、2 D、7. 如图,直线 与直线 的图象交于点P,那么关于x,y的二元一次方程组 的解是( )
A、 B、 C、 D、6. 已知 ,则 的立方根为( )A、1 B、 C、2 D、7. 如图,直线 与直线 的图象交于点P,那么关于x,y的二元一次方程组 的解是( )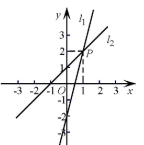 A、 B、 C、 D、8. 以方程组 的解为坐标的点 关于 轴对称的点的坐标是( )A、 B、 C、 D、9. 在抗击“新冠肺炎”的战役中,某品牌消毒液生产厂家计划向部分学校共捐赠13吨消毒液.如果这13吨消毒液的大瓶装(500克)与小瓶装(250克)两种产品分装的数量(按瓶计算)比为 .那么这两种产品应该各分装多少瓶?若设生产的消毒液应需分装 大瓶、 小瓶,则以下所列方程组正确的是( )A、 B、 C、 D、10. 港口 依次在同一条直线上,甲、乙两艘船同时分别从 两港出发,匀速驶向 港,甲、乙两船与 港的距离 (海里)与行驶时间 (小时)之间的函数关系如图所示,则下列说法正确的有( )
A、 B、 C、 D、8. 以方程组 的解为坐标的点 关于 轴对称的点的坐标是( )A、 B、 C、 D、9. 在抗击“新冠肺炎”的战役中,某品牌消毒液生产厂家计划向部分学校共捐赠13吨消毒液.如果这13吨消毒液的大瓶装(500克)与小瓶装(250克)两种产品分装的数量(按瓶计算)比为 .那么这两种产品应该各分装多少瓶?若设生产的消毒液应需分装 大瓶、 小瓶,则以下所列方程组正确的是( )A、 B、 C、 D、10. 港口 依次在同一条直线上,甲、乙两艘船同时分别从 两港出发,匀速驶向 港,甲、乙两船与 港的距离 (海里)与行驶时间 (小时)之间的函数关系如图所示,则下列说法正确的有( )① 两港之间的距离为60海里
②甲、乙两船在途中只相遇了一次
③甲船平均速度比乙船平均速度快30海里/时
④甲船到达 港时,乙船还需要一个小时才到达 港
⑤点 的坐标为
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 关于 的一次函数 的图象不经过第象限.12. 在某时段有 辆车通过一个雷达测速点,工作人员将测得的车速绘制成如图所示的条形统计图,则这 辆车的车速的中位数为 .
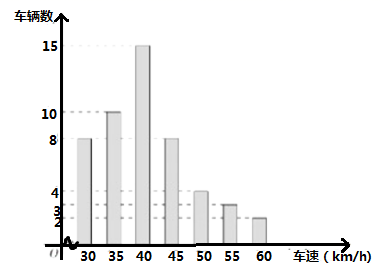 13. 如图,用大小、形状完全相同的长方形纸片在平面直角坐标系中摆成如图所示的图案,已知 ,则点 的坐标为.
13. 如图,用大小、形状完全相同的长方形纸片在平面直角坐标系中摆成如图所示的图案,已知 ,则点 的坐标为.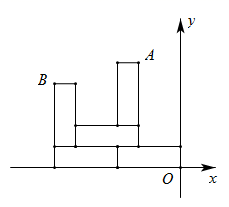
三、解答题
-
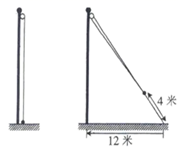
14. 计算: .15. 解方程组 .16. 已知一次函数 的图象经过点 ,求一次函数 的表达式.17. 如图,小东将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约4米,请算出旗杆的高度.
 18. 对于实数 、 ,定义关于“ ”的一种运算: ,例如 .(1)、求 的值;(2)、若 , ,求 的值.19. 已知 在平面直角坐标系中的位置如图所示,小方格都是边长为1的正方形.
18. 对于实数 、 ,定义关于“ ”的一种运算: ,例如 .(1)、求 的值;(2)、若 , ,求 的值.19. 已知 在平面直角坐标系中的位置如图所示,小方格都是边长为1的正方形.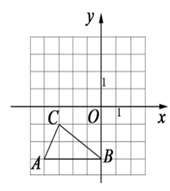 (1)、作出 关于 轴对称的 .(2)、判断 是不是直角三角形,并说明理由.20. 2020年12月12日是西安事变纪念日,某中学决定开展“铭记历史”主题演讲比赛,其中八(3)班要从甲、乙两名参赛选手中择优推荐一人参加校级决赛,他们预赛阶段的各项得分如下表:
(1)、作出 关于 轴对称的 .(2)、判断 是不是直角三角形,并说明理由.20. 2020年12月12日是西安事变纪念日,某中学决定开展“铭记历史”主题演讲比赛,其中八(3)班要从甲、乙两名参赛选手中择优推荐一人参加校级决赛,他们预赛阶段的各项得分如下表:项目
选手
演讲内容
演讲技巧
仪表形象
甲
95
90
85
乙
88
92
93
(1)、如果根据三项成绩的平均分确定推荐人选,请通过计算说明甲、乙两人谁会被推荐.(2)、如果根据演讲内容、演讲技巧、仪表形象按 的比例确定成绩,请通过计算说明甲、乙两人谁会被推荐.21. 关于 的二元一次方程组 的解也是二元一次方程 的解,求 的值.22. 由甲、乙两组各10名学生,进行趣味数学抢答比赛,共10道题.答对题数统计如下:答对题数
5
6
7
8
9
10
平均数
中位数
众数
方差
甲组学生数
1
0
1
5
2
1
8
8
8
乙组学生数
0
0
4
3
2
1
(1)、将表中的数据填写完整.(2)、根据所学的统计知识,从不同方面评价甲、乙两组选手的成绩.23. 近几年大部分家庭流行用不锈钢钢管做防盗窗,小芳家的防盗窗按设计要求,需要长为0.8米的钢管100根,及长为2.5米的钢管32根,两种长度的钢管粗细必须相同;并要求这些用料不能是焊接而成的,经市场调查,钢材市场中符合这种规格的钢管每根长均为6米.(1)、将一根长为6米的钢管进行裁剪(余料作废),有下面几种方法,请完成填空:方法①:只裁长为0.8米的钢管时,最多可裁根.
方法②:先裁下1根2.5米长的钢管,余下部分最多能裁0.8米长的钢管根.
方法③:先裁下2根2.5米长的钢管,余下部分最多能裁0.8米长的钢管根.
(2)、用(1)中的三种方法里面的两种进行结合来裁剪6米长的钢管,在尽量减少用料的情况下,如何裁剪才能得到所需要的相应数量的材料?24. 如图,直线 分别与 轴、 轴交于点 和点 ,直线 与 轴交于点 ,且两直线的交点为 .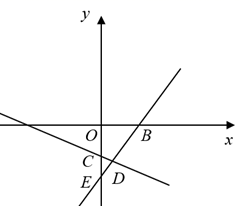 (1)、求点 的坐标.(2)、设点 ,且 ,若 和 的面积相等,求 的值.(3)、在(2)的条件下,以 为一腰作等腰 ,且点 在坐标轴上,请直接写出点 的坐标.
(1)、求点 的坐标.(2)、设点 ,且 ,若 和 的面积相等,求 的值.(3)、在(2)的条件下,以 为一腰作等腰 ,且点 在坐标轴上,请直接写出点 的坐标.