天津市七校2020-2021学年高三上学期数学期末联考试卷

试卷更新日期：2021-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 设集合 $M = [1, 2]$ ， $N = {x \in Z ∣ x^{2} - 2 x - 3 < 0}$ ，则 $M \cap N =$ （）

A、 $[1, 2]$ B、 ${- 1, 3}$ C、{1} D、 ${1, 2}$

查看试题解析
2. 对于实数a､b， $b < a < 0$ 是 $\frac{1}{b} > \frac{1}{a}$ 的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 函数 $f (x) = (x^{2} - 2 x) e^{x}$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
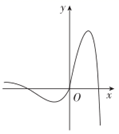4. 某学校组织部分学生参加体能测试，成绩的频率分布直方图如图，数据的分组依次是 $[20，40)$ ， $[40，60)$ ， $[60，80)$ ， $[80，100)$ .若低于60分的人数是18人，则参加体能测试的学生人数是（）

A、45 B、48 C、50 D、60

查看试题解析
5. 已知三棱锥 $A - B C D$ 的四个顶点A、B、C、D都在半径为 $\sqrt{3}$ 的球O的表面上，AC⊥平面 $B C D$ ，BD=3，BC=2， $C D = \sqrt{5}$ ，则该三棱锥的体积为（）

A、 $\frac{\sqrt{15}}{3}$ B、 $\frac{2 \sqrt{15}}{3}$ C、 $\frac{\sqrt{15}}{6}$ D、 $\sqrt{15}$

查看试题解析
6. 已知定义在R上的函数 $f (x)$ 满足 $f (x + 6) = f (x), y = f (x + 3)$ 为偶函数，若 $f (x)$ 在 $(0, 3)$ 内单调递减．则下面结论正确的是（）

A、 $f (10) < f (e^{\frac{1}{2}}) < f (\ln 2)$ B、 $f (e^{\frac{1}{2}}) < f (\ln 2) < f (10)$ C、 $f (\ln 2) < f (10) < f (e^{\frac{1}{2}})$ D、 $f (\ln 2) < f (e^{\frac{1}{2}}) < f (10)$

查看试题解析
7. 已知双曲线 $C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的左焦点为 $F$ ，以 $O F$ 为直径的圆与双曲线 $C$ 的渐近线交于不同原点 $O$ 的 $A ， B$ 两点，若四边形 $A O B F$ 的面积为 $\frac{1}{2} (a^{2} + b^{2})$ ，则双曲线 $C$ 的渐近线方程为（）

A、 $y = \pm \frac{\sqrt{2}}{2} x$ B、 $y = \pm \sqrt{2} x$ C、 $y = \pm x$ D、 $y = \pm 2 x$

查看试题解析
8. 已知函数 $f (x) = 2 (| \cos x | + \cos x) \cdot \sin x$ ，给出下列四个命题：（）
① $f (x)$ 的最小正周期为 $π$ ② $f (x)$ 的图象关于直线 $x = \frac{π}{4}$ 对称③ $f (x)$ 在区间 $[- \frac{π}{4} ， \frac{π}{4}]$ 上单调递增④ $f (x)$ 的值域为 $[- 2 ， 2]$

其中所有正确的编号是（）

A、②④ B、①③④ C、③④ D、②③

查看试题解析
9. 已知函数 $f (x) = {\begin{array}{l} x^{2} + (4 a - 3) x + 3 a, x < 0, \\ \log_{a} (x + 1) + 1, x \geq 0 \end{array}$ （ $a > 0$ ，且 $a \neq 1$ ）在 $R$ 上单调递减，且关于x的方程 $| f (x) | = 2 - x$ 恰有两个不相等的实数解，则 $a$ 的取值范围是（）

A、 $(0, \frac{2}{3}]$ B、[ $\frac{2}{3}$ ， $\frac{3}{4}$ ] C、[ $\frac{1}{3}$ ， $\frac{2}{3}$ ] $\cup$ { $\frac{3}{4}$ } D、[ $\frac{1}{3}$ ， $\frac{2}{3}$ ） $\cup$ { $\frac{3}{4}$ }

查看试题解析

二、填空题

10. $i$ 是虚数单位，复数 $\frac{- 1 + 3 i}{1 + 2 i}$ = .

查看试题解析
11. ${(x^{3} + \frac{1}{x})}^{7}$ 的展开式中 $x^{5}$ 的系数是.（用数字填写答案）

查看试题解析
12. 已知圆C：x²+y²﹣2x﹣2y﹣6=0.直线l过点(0，3)，且与圆C交于A､B两点，|AB|=4，则直线l的方程.

查看试题解析
13. 已知实数 $a > 0$ ， $b > 0$ ， $\frac{1}{a} + \frac{2}{b} = 1$ ，则 $\frac{4 a}{a - 1} + \frac{3 b}{b - 2}$ 的最小值是.

查看试题解析
14. 一个口袋里装有大小相同的5个小球，其中红色两个，其余3个颜色各不相同 $.$ 现从中任意取出3个小球，其中恰有2个小球颜色相同的概率是；若变量X为取出的三个小球中红球的个数，则X的数学期望 $E (X) =$ ．

查看试题解析
15. 已知扇形 $A O B$ 半径为 $1$ ， $∠ A O B = 60 °$ ，弧 $A B$ 上的点 $P$ 满足 $\overset{⇀}{O P} = λ \overset{⇀}{O A} + μ \overset{⇀}{O B} (λ ， μ \in R)$ ，则 $λ + μ$ 的最大值是； $\overset{⇀}{P A} \cdot \overset{⇀}{P B}$ 最小值是；

查看试题解析

三、解答题

16. 在 $△ A B C$ 中，角 $A, B, C$ 的对边分别为 $a, b, c$ ，已知 $B = 45^{°}$ ， $b = \sqrt{10}$ ， $\tan C = \frac{1}{2}$
（I）求边 $a$ ；

（II）求 $\sin (2 A - B)$ .

查看试题解析
17. 如图，四边形 $A B C D$ 与 $B D E F$ 均为菱形， $F A = F C$ ， $A B = 2$ ，且 $∠ D A B = ∠ D B F = 60^{\circ}$ .

(1)、求证： $A C ⊥$ 平面 $B D E F$ ；

(2)、求钝二面角 $E - A F - B$ 的余弦值；

(3)、若 $M$ 为线段 $D E$ 上的一点，满足直线 $A M$ 与平面 $A B F$ 所成角的正弦值为 $\frac{2 \sqrt{30}}{15}$ ，求线段 $D M$ 的长.

查看试题解析
18. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左右焦点分别是 $F_{1}$ 和 $F_{2}$ ，离心率为 $\frac{1}{2}$ ，点P在椭圆E上，且 $△ P F_{1} F_{2}$ 的面积的最大值为 $\sqrt{3}$ .

(1)、求椭圆C的方程；

(2)、直线l过椭圆C右焦点 $F_{2}$ ，交该椭圆于A､B两点，AB中点为Q，射线OQ交椭圆于P，记 $△ A O Q$ 的面积为 $S_{1}$ ， $△ B P Q$ 的面积为 $S_{2}$ ，若 $S_{2} = 3 S_{1}$ ，求直线l的方程.

查看试题解析
19. 已知等比数列 ${a_{n}}$ 的公比 $q > 0$ ，且满足 $a_{1} + a_{2} = 6 a_{3}$ ， $a_{4} = 4 a_{3}^{2}$ ，数列 ${b_{n}}$ 的前 $n$ 项和 $S_{n} = \frac{n (n + 1)}{2}$ ， $n \in N *$ .

(1)、求数列 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、设 $c_{n} = {\begin{array}{l} \frac{3 b_{n} + 8}{b_{n} b_{n + 2}} \cdot a_{n + 2}, n 为奇数 \\ a_{n} b_{n}, n 为偶数 \end{array}$ ，求数列 ${c_{n}}$ 的前 $2 n$ 项和 $T_{2 n}$ .

查看试题解析
20. 已知函数 $f (x) = \frac{e^{x}}{x} - \ln x + x - 2 a$ ， $a \in R$ ．

(1)、求函数 $f (x)$ 的单调区间；

(2)、若函数 $f (x)$ 有两个不同的零点 $x_{1}$ ， $x_{2}$ ，
（i）求 $a$ 的取值范围；

（ii）证明： $| x_{2} - x_{1} | < \frac{4 a^{2} - 2 a - 1}{2 a - 1}$ ．

查看试题解析