天津市南开区2020-2021学年高三上学期数学期末考试试卷
试卷更新日期:2021-01-26 类型:期末考试
一、单选题
-
1. 若集合 , ,则 等于( )A、 B、 C、 D、{2}2. “ ”是“ ”( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分又不必要条件3. 函数 的定义域为( )A、 B、 C、 D、4. 已知等比数列 满足 , ,则 的值为( )A、 B、 C、1 D、25. 函数 的图像经过怎样的平移变换得到函数 的图像( )A、向左平移 个单位长度 B、向左平移 个单位长度 C、向右平移 个单位长度 D、向右平移 个单位长度6. 已知圆 截直线 所得弦的长度为4,则实数a的值是(A、-2 B、-4 C、-6 D、-87. 已知函数 ,且 , , ,则 、 、 的大小关系为( )A、 B、 C、 D、8. 已知抛物线 的焦点为 , 为 上一点且在第一象限,以 为圆心, 为半径的圆交 的准线于 , 两点,且 , , 三点共线,则 ( )A、12 B、9 C、6 D、39. 已知 ,若函数 有三个或者四个零点,则函数 的零点个数为( )A、1或2 B、2 C、1或0 D、0或1或2
二、填空题
-
10. 已知复数 ,则 .11. 曲线 在点 处的切线方程是.12. 已知如图所示的多面体 中,四边形ABCD是菱形,四边形BDEF是矩形,ED⊥平面ABCD,∠BAD= .若BF=BD=2,则多面体的体积 .
 13. 已知正数 , 满足 ,则 的最小值为.14. 已知双曲线的方程为 ,则此双曲线的离心率为 , 其焦点到渐近线的距离为 .15. 如图,在边长1为正方形 中, , 分别是 , 的中点,则 , 若 ,则 .
13. 已知正数 , 满足 ,则 的最小值为.14. 已知双曲线的方程为 ,则此双曲线的离心率为 , 其焦点到渐近线的距离为 .15. 如图,在边长1为正方形 中, , 分别是 , 的中点,则 , 若 ,则 .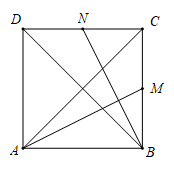
三、解答题
-
16. 在 中,角 , , 所对的边分别为 , , ,且 , , 的面积为 .(1)、求 , , 的值;(2)、求 的值.17. 如图,直二面角 中,四边形 是边长为2的正方形, , 为 上的点,且 平面 .
 (1)、求证: 平面 ;(2)、求二面角 的正弦值;(3)、求点 到平面 的距离.18. 已知点F为椭圆 (a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.(1)、求椭圆的标准方程;(2)、若M、N在椭圆上但不在坐标轴上,且直线AM∥直线BN,直线AN、BM的斜率分别为k1和k2 , 求证:k1•k2=e2﹣1(e为椭圆的离心率).
(1)、求证: 平面 ;(2)、求二面角 的正弦值;(3)、求点 到平面 的距离.18. 已知点F为椭圆 (a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.(1)、求椭圆的标准方程;(2)、若M、N在椭圆上但不在坐标轴上,且直线AM∥直线BN,直线AN、BM的斜率分别为k1和k2 , 求证:k1•k2=e2﹣1(e为椭圆的离心率).