浙教版备考2021年中考数学一轮复习专题14——二次函数的图象与性质

试卷更新日期：2021-01-26 类型：一轮复习

进入出卷网下载

一、单选题

1. 下列关系式中，属于二次函数的是（）

A、 $y = 3 x^{2} - 2 x - 1$ B、 $y = - 4 x$ C、 $y = x + 5$ D、 $y = \frac{- 1}{x}$

查看试题解析
2. 抛物线 $y = x^{2} + 3$ 的顶点坐标是（　　）

A、（0，3） B、（3，0） C、（0，﹣3） D、（﹣3，0）

查看试题解析
3. 抛物线 $y = 2 {(x + 1)}^{2} - 3$ 的顶点坐标是（）

A、 $(1 ， - 3)$ B、 $(1 ， 3)$ C、 $(- 1 ， - 3)$ D、 $(- 1 ， 3)$

查看试题解析
4. 抛物线 $y = {(x + 2)}^{2} - 5$ 的对称轴是（）

A、y轴 B、直线x=-2 C、直线x=2 D、直线x=-5

查看试题解析
5. 二次函数 $y = - 3 x^{2} + 6 x + 5$ 的最大值是（）

A、0 B、5 C、8 D、10

查看试题解析
6. 已知 $b < 0$ 时，二次函数 $y = a x^{2} + b x + a^{2} - 4$ 的图象如下列四个图之一所示.根据图象分析 $a$ 的值等于（）.

A、-2 B、-1 C、1 D、2

查看试题解析
7. 根据下列表格的对应值：判断方程ax²＋bx＋c＝0(a≠0)的一个根x的大致范围是（）

x

6.17

6.18

6.19

6.20

ax²＋bx＋c

−0.03

−0.01

0.02

0.04

A、6.19<x<6.20 B、6.18<x<6.19 C、6.17<x<6.18 D、6<x<6.17

查看试题解析
8. 点 $P_{1} (- 2, y_{1}), P_{2} (2, y_{2}), P_{3} (4, y_{3})$ 均在二次函数 $y = - x^{2} + 2 x + c$ 的图象上，则 $y_{1}, y_{2}, y_{3}$ 的大小关系是（）

A、 $y_{2} > y_{3} > y_{1}$ B、 $y_{2} > y_{1} = y_{3}$ C、 $y_{1} = y_{3} > y_{2}$ D、 $y_{1} = y_{2} > y_{3}$

查看试题解析
9. 平面直角坐标系中，将抛物线 $y = - x^{2}$ 先向右平移1个单位，再向上平移2个单位，得到的抛物线的解析式是（）

A、 $y = {(x + 1)}^{2} + 2$ B、 $y = {(x - 1)}^{2} + 2$ C、 $y = - {(x - 1)}^{2} + 2$ D、 $y = - {(x - 1)}^{2} - 2$

查看试题解析
10. 在平面直角坐标系中，二次函数y=ax²+bx+c(a≠0)的图象如图所示，现给出以下结论：①abc <0；②c+2a<0；③9a-3b+c=0； ④a-b≥m(am+b) (m为实数)：⑤4ac-b²<0。
其中错误结论的个数有（）

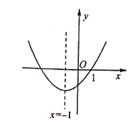A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 抛物线 $y = - 2 x^{2} + x + 1$ 的对称轴是．

查看试题解析
12. 抛物线 $y = x^{2} - 2 x + 3$ 的图象与y轴的交点坐标为．

查看试题解析
13. 如果抛物线 $y = (4 + k) x^{2} + 2 x + 1$ 的开口向下，那么k的取值范围是．

查看试题解析
14. 若实数 $a 、 b$ 满足 $a + b^{2} = 2$ ，则 $a$ 满足的范围， $a^{2} + 5 b^{2}$ 的最小值为.

查看试题解析
15. 已知抛物线解析式为y=x²-2x-3（2≤x≤5），则函数的最小值为．

查看试题解析
16. 如图，把抛物线y=-x²+2向右平移1个单位长度，则曲线AB扫过的面积（图中阴影部分）是.

查看试题解析
17. 如图，是抛物线y=ax2+bx+c（a≠0）的一部分，已知抛物线的对称轴为x=2，与x轴的一个交点是（-1，0），则方程ax2+bx+c=0（a≠0）的两根是

查看试题解析
18. 已知二次函数 $y = - 2 {(x - 1)}^{2} + k$ 的图象上有 $A (- \sqrt{7}, y_{1})$ ， $B (2, y_{2})$ ， $C (3, y_{3})$ 三个点.用“＜”连接 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的结果是.

查看试题解析
19. 如图，在平面直角坐标系中，过点P(m，0)作x轴的垂线，分别交抛物线y=x²+ $\frac{3}{2}$ x+2和直线y= $- \frac{1}{2}$ x-2于点A和点C，以线段AC为对角线作正方形ABCD，则当正方形ABCD的面积最小时m的值为。

查看试题解析

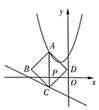
三、综合题

20. 已知二次函数的顶点坐标为（4，－2），且其图象经过点（5，1），求此二次函数的解析式．

查看试题解析
21. 如图，二次函数y=ax²+bx的图像经过点A(2，4)与B(6，0)。

(1)、求a，b的值；

(2)、若点C是该二次函数的最高点，求△OBC的面积。

查看试题解析
22. 已知二次函数y＝2x²+4x﹣6，

(1)、将二次函数的解析式化为y＝a（x﹣h）²+k的形式．

(2)、写出二次函数图象的开口方向、对称轴、顶点坐标．

查看试题解析
23. 在二次函数y=ax2+bx+c（a≠0）中，函数y与自变量x的部分对应值如表：

x

…

0

1

2

3

4

…

y

…

3

0

−1

0

m

…

(1)、求这个二次函数的解析式及m的值；

(2)、在平面直角坐标系中，用描点法画出这个二次函数的图象（不用列表）；

(3)、当y<3时，则x的取值范围是．

查看试题解析
24. 已知抛物线y＝ax²+bx+c与x轴交于点A（1，0），B（3，0），且过点C（0，﹣3）．

(1)、求抛物线的解析式和顶点坐标；

(2)、将该抛物线向左平移个单位长度后，可使平移后的抛物线的顶点落在直线y＝﹣x上，并写出平移后抛物线的解析式：；

(3)、观察图象，写出关于x的不等式ax²+bx+c+3＞0的解集．

查看试题解析
25. 如图所示，已知抛物线 $y = a x^{2} (a \neq 0)$ 与一次函数 $y = k x + b$ 的图象相交于 $A (- 1 ， - 1)$ ， $B (2 ， - 4)$ 两点，点 $P$ 是抛物线上不与 $A$ ， $B$ 重合的一个动点.

(1)、请直接写出 $a$ ， $k$ ， $b$ 的值；

(2)、当点 $P$ 在直线 $A B$ 上方时，过点 $P$ 作 $y$ 轴的平行线交直线 $A B$ 于点 $C$ ，设点 $P$ 的横坐标为 $m$ ， $P C$ 的长度为 $L$ ，求出 $L$ 关于 $m$ 的解析式；

(3)、在（2）的基础上，设 $Δ P A B$ 面积为 $S$ ，求出 $S$ 关于 $m$ 的解析式，并求出当 $m$ 取何值时， $S$ 取最大值，最大值是多少？

查看试题解析

x	6.17	6.18	6.19	6.20
ax²＋bx＋c	−0.03	−0.01	0.02	0.04

x	…	0	1	2	3	4	…
y	…	3	0	−1	0	m	…