浙教版备考2021年中考数学一轮复习专题13——反比例函数的图象与性质及应用

试卷更新日期：2021-01-26 类型：一轮复习

进入出卷网下载

一、单选题

1. 若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $(2 ， - 3)$ ，则k的值为（）

A、5 B、 $- 5$ C、6 D、 $- 6$

查看试题解析
2. 对于反比例函数y= $\frac{6}{x}$ 的图象的对称性叙述错误的是（）

A、关于原点中心对称 B、关于直线y=x对称 C、关于直线y=-x对称 D、关于x轴对称

查看试题解析
3. 若点A(-1，y₁)，B(2，y₂)，C(-3，y₃)在反比例函数y= $\frac{6}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₃<y₂<y₁ B、y₂<y₁<y₃ C、y₁<y₃<y₂ D、y₁<y₂<y₃

查看试题解析
4. 下列函数y是x的反比例函数的是（）

A、y＝2x B、y＝ $- \frac{2}{3}$ x^﹣¹ C、y＝ $- \frac{2}{2 x - 1}$ D、y＝﹣x

查看试题解析
5. 如图，在轴正半轴上依次截取 $O A_{1} = A_{1} A_{2} = A_{2} A_{3} = ... = A_{n - 1} A_{p} = 1$ ，过点 $A_{1} 、 A_{2} 、 A_{3} 、 ...... A_{n}$ 分别作x轴的垂线，与反比例函数 $y = \frac{2}{x} (x > 0)$ 交于点 $P_{1} 、 P_{2} 、 P_{3} 、 ...... P_{n}$ ，连接 $P_{1} P_{2} 、 P_{2} P_{3} ... P_{n - 1} P_{n}$ 过点 $P_{2} 、 P_{3} 、 ...... P_{n}$ 分别向 $P_{1} A_{1} 、 P_{2} A_{2} 、 ... 、 P_{n- 1} A_{n - 1}$ 作垂线段，构成的一系列直角三角形（图中阴影部分）的面积和等于（）

A、 $2^{n}$ B、 $\frac{n - 1}{n}$ C、 $2 n + 1$ D、 $\frac{n + 2}{2 n}$

查看试题解析
6. 在一个可以改变容积的密闭容器内，装有一定质量m的某种气体，当改变容积V时，气体的密度ρ也随之改变.p与V在一定范围内满足，它的图象如图所示，则该气体的质量m为（）

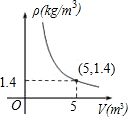A、1.4kg B、5kg C、6.4kg D、7kg

查看试题解析
7. 如图，在平面直角坐标系中，将一块含有45°的直角三角板按照如图方式摆放，顶点A、B的坐标为（1，4）、（4，1），直角顶点C的坐标为（4，4），若反比例函数 $y = \frac{k}{x}$ $（ x > 0 ）$ 的图象与直角三角板的边有交点，则k的取值范围为（）

A、 $4 \leq k \leq 8$ B、 $\frac{25}{4} \leq k \leq 8$ C、 $4 \leq k \leq 16$ D、 $\frac{25}{4} \leq k \leq 16$

查看试题解析
8. 如图，点A，点B分别在反比例函数 $y = \frac{2}{x} (x > 0)$ 和反比例函数 $y = - \frac{4}{x} (x < 0)$ 的图象上，AB∥x轴，交y轴与点C，且∠AOB=90°，则AC：CB等于（）

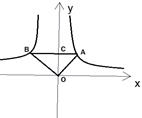A、1：2 B、1：3 C、1：4 D、1： $\sqrt{2}$

查看试题解析
9. 如图，平行于x轴的直线与函数y＝ $\frac{k_{1}}{x}$ （k₁＞0，x＞0），y＝ $\frac{k_{2}}{x}$ （k₂＞0，x＞0）的图象分别相交于A，B两点，点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为6，则k₁﹣k₂的值为（　　）

A、12 B、﹣12 C、6 D、﹣6

查看试题解析

二、填空题

10. 如果反比例函数 $y = \frac{2 - k}{x}$ （ $k$ 为常数）的图象在二、四象限，那么 $k$ 的取值范围是

查看试题解析
11. 近视眼镜的度数y（度）与镜片焦距x（m）成反比例，已知400度近视眼镜镜片的焦距为0.25m，则眼镜度数与镜片焦距之间的函数关系式为.

查看试题解析
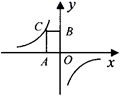
12. 如图，已知点C为反比例函数 $y = - \frac{6}{x}$ 上的一点，过点C向坐标轴引垂线，垂足分别为A、B，那么四边形AOBC的面积为.

查看试题解析
13. 若反比例函数y₁＝ $\frac{k}{x}$ （k＞0，x＞0）的图象与直线y₂＝x﹣1在第一象限内的交点为A，点A的横坐标为m，且满足2＜m＜3，则k的取值范围是.

查看试题解析
14. 如图，正比例函数与反比例函数的图象相交于A、B两点，分别以A、B两点为圆心，画与y轴相切的两个圆，若点A的坐标为(1，2)，则图中两个阴影面积的和是．

查看试题解析
15. 如图，经过原点的直线与反比例函数y= $\frac{k}{x}$ (k>0)相交于A，B两点，BC⊥x轴。若△ABC的面积为4，则k的值为。

查看试题解析

三、综合题

16. 已知反比例函数 $y = \frac{k}{x}$ （ $k \neq 0$ ）的图象经过点A（2，3）.

(1)、求函数解析式；

(2)、当x＝－4时，求反比例函数 $y = \frac{k}{x}$ 的值.

查看试题解析
17. 如图，函数的图象 $y_{1} = k_{1} x + b$ 与函数 $y_{2} = \frac{k_{2}}{x} (x > 0)$ 的图象交于点A（2，1）、B，与y轴交于C（0，3）

(1)、求函数y₁的表达式和点B的坐标；

(2)、观察图象，比较当x＞0时y₁与y₂的大小．

查看试题解析
18. 如图，一次函数y=kx+b的图象与反比例函数y= $\frac{m}{x}$ 的图象相交于A(1，2)，B(n， -1)两点。

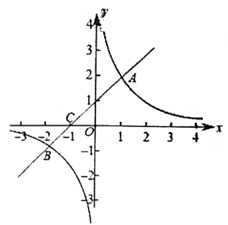(1)、求一次函数和反比例函数的表达式；

(2)、直线AB交x轴于点C，点P是x轴上的点，若△ACP的面积是4，求点P的坐标。

查看试题解析
19. 方方驾驶小汽车匀速地从A地行使到B地，行驶里程为480千米，设小汽车的行使时间为t（单位：小时），行使速度为v（单位：千米/小时），且全程速度限定为不超过120千米/小时.

(1)、求v关于t的函数表达式；

(2)、方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点（含12点48分和14点）间到达B地，求小汽车行驶速度v的范围.

②方方能否在当天11点30分前到达B地？说明理由.

查看试题解析

20. 在函数的学习中，我们经历了“确定函数表达式——画函数图象——利用函数图象研究函数性质——利用图像解决问题”的学习过程.我们可以借鉴这种方法探究函数

y = \frac{4}{x - 1}

的图像性质.

(1)、补充表格，并画出函数的图象

①列表：

x	…	-3	-1	0	2	3	5	…
y	…	-1	-2	-4	4		1	…

②描点并连线，画图.

(2)、观察图像，写出该函数图象的一个增减性特征：；

(3)、函数

y = \frac{4}{x - 1}

的图像是由函数

y = \frac{4}{x}

的图像如何平移得到的？，其对称中心的坐标为；

(4)、根据上述经验，猜一猜函数

y = \frac{4}{x - 1} + 2

的图像大致位置，结合图像直接写出y≥3时，x的取值范围.

查看试题解析

21. 如图1和图2，在△ABC中，AB＝13，BC＝14， $\frac{B H}{A B} = \frac{5}{13}$ .

(1)、探究：
如图1，AH⊥BC于点H，则AH＝， AC＝， △ABC的面积 $S_{Δ A B C}$ ＝.

(2)、拓展：如图2，点D在AC上（可与点A、C重合），分别过点A、C作直线BD的垂线，垂足为E、F，设BD＝x，AE＝m，CF＝n，（当点D与A重合时，我们认为 $S_{Δ A B D}$ ＝0）.
用含x、m或n的代数式表示 $S_{Δ A B D}$ 及 $S_{Δ C B D}$ ；

(3)、求（m+n）与x的函数关系式，并求（m+n）的最大值和最小值；

(4)、对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围.
发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值.

查看试题解析