浙教版备考2021年中考数学一轮复习专题12——一次函数的应用
试卷更新日期:2021-01-26 类型:一轮复习
一、单选题
-
1. 直线 向上平移 个单位得到的直线解析式是( )A、 . B、 C、 D、2. 一个正比例函数的图象经过点 ,它的表达式为( )A、 B、 C、 D、3. 直线l是以二元一次方程 的解为坐标所构成的直线,则该直线不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 一次函数y=kx-b的图象如图所示,则关于x的方程kx-b=0的解是( )
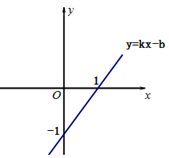 A、(1,0) B、(0,-1) C、x=1 D、x=﹣15. 如图,直线 与 ( 且a,b为常数)的交点坐标为(3,﹣1),则关于x的不等式 的解集为( )
A、(1,0) B、(0,-1) C、x=1 D、x=﹣15. 如图,直线 与 ( 且a,b为常数)的交点坐标为(3,﹣1),则关于x的不等式 的解集为( ) A、x≥﹣1 B、x≥3 C、x≤﹣1 D、x≤36. 一根蜡烛长20cm , 点燃后每小时燃烧5cm燃烧时剩下的高度h(cm)与时间t(小时)的关系图象表示是( )A、
A、x≥﹣1 B、x≥3 C、x≤﹣1 D、x≤36. 一根蜡烛长20cm , 点燃后每小时燃烧5cm燃烧时剩下的高度h(cm)与时间t(小时)的关系图象表示是( )A、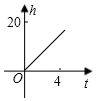 B、
B、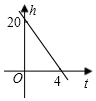 C、
C、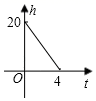 D、
D、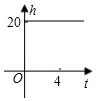 7. 甲、乙两车同时从A地出发,沿同一路线各自匀速向B地行驶,甲到达B地停留1小时后按原路以另一速度匀速返回,直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则下列结论错误的是( )
7. 甲、乙两车同时从A地出发,沿同一路线各自匀速向B地行驶,甲到达B地停留1小时后按原路以另一速度匀速返回,直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则下列结论错误的是( )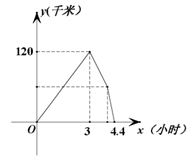 A、行驶3小时后,两车相距120千米 B、甲车从A到B的速度为100千米/小时 C、甲车返回是行驶的速度为95千米/小时 D、A,B两地之间的距离为300千米8. 弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:
A、行驶3小时后,两车相距120千米 B、甲车从A到B的速度为100千米/小时 C、甲车返回是行驶的速度为95千米/小时 D、A,B两地之间的距离为300千米8. 弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:x/kg
0
1
2
3
4
5
y/cm
10
10.5
11
11.5
12
12.5
下列说法错误的是( )
A、x与y都是变量,且x是自变量,y是因变量 B、弹簧不挂重物时的长度为0 cm C、物体质量每增加1 kg,弹簧长度y增加0.5 cm D、所挂物体质量为7 kg时,弹簧长度为13.5 cm9. 如图,已知直线y= 与x轴、y轴分别交于B、C两点,A是以D(0,2)为圆心,2为半径的圆上一动点,连结AC、AB,则△ABC面积的最小值是( )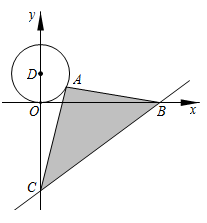 A、30 B、29 C、28 D、2710. 如图,等腰Rt△ABC中,BC= ,以边AC为斜边向右做等腰Rt△ACD,点E是线段CD的中点,连接 AE.作线段CE关于直线AC的对称线段CF,连接BF,并延长BF交线段AE于点G,则线段BG长为( )
A、30 B、29 C、28 D、2710. 如图,等腰Rt△ABC中,BC= ,以边AC为斜边向右做等腰Rt△ACD,点E是线段CD的中点,连接 AE.作线段CE关于直线AC的对称线段CF,连接BF,并延长BF交线段AE于点G,则线段BG长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 根据图象,不等式kx>﹣x+3的解集是.
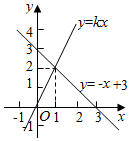 12. 长方形的周长为10 ,其中一边为 (其中 ),另一边为 ,则 关于 的函数表达式为.13. 如图所示:已知直线 : 交x轴于点A,交y轴于点 B.直线 经过点B且与x轴交于点C(2 , 0)在直线 上取一点M,使得M到 的 距离为2.则M点的坐标为.
12. 长方形的周长为10 ,其中一边为 (其中 ),另一边为 ,则 关于 的函数表达式为.13. 如图所示:已知直线 : 交x轴于点A,交y轴于点 B.直线 经过点B且与x轴交于点C(2 , 0)在直线 上取一点M,使得M到 的 距离为2.则M点的坐标为.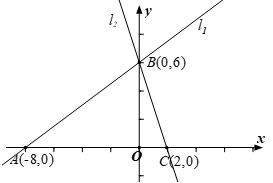 14. 一次函数 的图像如图所示,观察图像可得到关于 的方程 的解是 .
14. 一次函数 的图像如图所示,观察图像可得到关于 的方程 的解是 . 15. 若函数y=ax+b(a<0)的图象如图所示,则不等式ax+b≥0的解集是 .
15. 若函数y=ax+b(a<0)的图象如图所示,则不等式ax+b≥0的解集是 .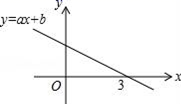 16. 如图,已知直线a:y=x,直线b:y=- x和点P(1,0),过点P作y轴的平行线交直线a于点P1 , 过点P1作x轴的平行线交直线b于点p2 , 过点p2作y轴的平行线交直线a于点p3 , 过点p3作x轴的平行线交直线b于点p4 , …,按此作法进行下去,则点P2021的横坐标为.
16. 如图,已知直线a:y=x,直线b:y=- x和点P(1,0),过点P作y轴的平行线交直线a于点P1 , 过点P1作x轴的平行线交直线b于点p2 , 过点p2作y轴的平行线交直线a于点p3 , 过点p3作x轴的平行线交直线b于点p4 , …,按此作法进行下去,则点P2021的横坐标为.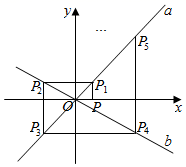 17. 十一黄金周,小明和小亮乘甲车从沙坪坝出发,以一定的速度匀速前往铁山坪体验“飞越丛林”.出发15分钟后,小明发现忘带身份证和钱包,便下车换乘乙车匀速回家去取(小明换车、取身份证和钱包的时间忽略不计),小亮仍乘甲车并以原速继续前行,小明回家取了身份证和钱包后,为节约时间,又立即乘乙车以原来速度的 倍匀速按原路赶往铁山坪,由于国庆期间车流量较大,在小明乘乙车以加速后的速度匀速赶往铁山坪期间,甲车恰好因故在途中持续堵塞了5分钟,结果乙车先到达目的地.甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的部分图象如图所示,则乙车出发小时到达目的地.
17. 十一黄金周,小明和小亮乘甲车从沙坪坝出发,以一定的速度匀速前往铁山坪体验“飞越丛林”.出发15分钟后,小明发现忘带身份证和钱包,便下车换乘乙车匀速回家去取(小明换车、取身份证和钱包的时间忽略不计),小亮仍乘甲车并以原速继续前行,小明回家取了身份证和钱包后,为节约时间,又立即乘乙车以原来速度的 倍匀速按原路赶往铁山坪,由于国庆期间车流量较大,在小明乘乙车以加速后的速度匀速赶往铁山坪期间,甲车恰好因故在途中持续堵塞了5分钟,结果乙车先到达目的地.甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的部分图象如图所示,则乙车出发小时到达目的地.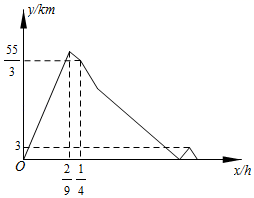
三、综合题
-
18. 如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),与x轴交于B点。
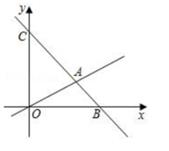 (1)、求直线AC的解析式;(2)、求△AOB的面积。19. 小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,请根据图中给出的信息,解答下列问题:
(1)、求直线AC的解析式;(2)、求△AOB的面积。19. 小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,请根据图中给出的信息,解答下列问题: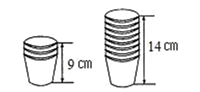 (1)、求整齐叠放在一起的纸杯的高度y(㎝)与纸杯的个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);(2)、若把100个纸杯整齐的叠放在一起,则它的高度是多少?20. 现计划把一批货物用一列火车运往某地.已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元.(1)、设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并写出自变量x的取值范围;(2)、已知A型车厢数不少于B型车厢数,估计运输总费用不低于276000元,问符合条件的运送方案中哪种方案运费最低?21. 某电脑经销商,今年二,三月份A型和B型电脑的销售情况,如下表所示:
(1)、求整齐叠放在一起的纸杯的高度y(㎝)与纸杯的个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);(2)、若把100个纸杯整齐的叠放在一起,则它的高度是多少?20. 现计划把一批货物用一列火车运往某地.已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元.(1)、设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并写出自变量x的取值范围;(2)、已知A型车厢数不少于B型车厢数,估计运输总费用不低于276000元,问符合条件的运送方案中哪种方案运费最低?21. 某电脑经销商,今年二,三月份A型和B型电脑的销售情况,如下表所示:A型(台)
B型(台)
利润(元)
二月份
15
20
4500
三月份
20
10
3500
(1)、直接写出每台A型电脑和B型电脑的销售利润分别为;(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.①求y与x的关系式;
②该商店购进A型、B型各多少台,才能使销售利润最大?
(3)、实际进货时,厂家对A型电脑出厂价下调 元,且限定商店最多购进A型电脑60台.若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案.22. 疫情发生后,口罩成了人们生活的必需品.某药店销售A,B两种口罩,今年3月份的进价如下表:A种口罩
B种口罩
进价(元/包)
12
28
已知B种口罩每包售价比A种口罩贵20元,9包A种口罩和4包B种口罩总售价相同。
(1)、求A种口罩和B种口罩每包售价。(2)、若该药店3月份购进A种和B种口罩共1500包进行销售,且B种口罩数量不超过A种口罩的 ,若所进口罩全部售出,则应该购进A种口罩多少包,才能使利润最大,并求出最大利润。(3)、为满足不同顾客的需求,该药店准备4月份新增购进进价为每包10元的C种口罩,A种和B种口罩仍按需购进,进价与3月份相同,A种口罩的数量是B种口罩的4倍,共花费12000元,则该店至少可以购进三种口罩共多少包?23. 如图,直线l1:y=x和直线l2:y=kx+3交于点A(2,2),P(t,0)是x轴上一动点,过点P作平行于y轴的直线,使其与直线l1和直线l2分别交于点D,E.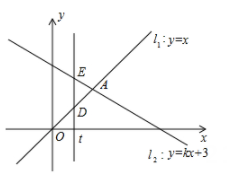 (1)、求k的值.(2)、用t表示线段DE的长.(3)、点M是y轴上一动点,当△MDE是等腰直角三角形时,求出t的值及点M的坐标.
(1)、求k的值.(2)、用t表示线段DE的长.(3)、点M是y轴上一动点,当△MDE是等腰直角三角形时,求出t的值及点M的坐标.