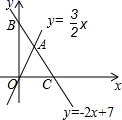浙教版备考2021年中考数学一轮复习专题11——一次函数的图象与性质
试卷更新日期:2021-01-26 类型:一轮复习
一、单选题
-
1. 下列函数中,不是一次函数的是( )A、 B、 C、 D、2. 已知点P(a,-b)在第一象限,则直线y=ax+b经过的象限为 ( )A、第一、二、三象限 B、第一、三、四象限 C、第二、三、四象限 D、第一、二、四象限3. 正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=x﹣k的图象大致是( )A、
 B、
B、 C、
C、 D、
D、 4. 已知油箱中有油25升,每小时耗油5升,则剩油量P(升)与耗油时间t(小时)之间的函数关系式为( )A、P=25+5t B、P=25-5t C、P= D、P=5t-255. 直线y=2x﹣1在 轴上的截距是( )A、1 B、﹣1 C、2 D、﹣26. 已知正比例函数 的图像上有两点且 , ,且x1>x2 , 则y1与y2的大小关系是( )A、 B、 C、 D、不能确定.7. 已知 是关于x的正比例函数,则m的值为( )A、2 B、1 C、0或2 D、08. 若式子 有意义,则一次函数 的图象可能是( )A、
4. 已知油箱中有油25升,每小时耗油5升,则剩油量P(升)与耗油时间t(小时)之间的函数关系式为( )A、P=25+5t B、P=25-5t C、P= D、P=5t-255. 直线y=2x﹣1在 轴上的截距是( )A、1 B、﹣1 C、2 D、﹣26. 已知正比例函数 的图像上有两点且 , ,且x1>x2 , 则y1与y2的大小关系是( )A、 B、 C、 D、不能确定.7. 已知 是关于x的正比例函数,则m的值为( )A、2 B、1 C、0或2 D、08. 若式子 有意义,则一次函数 的图象可能是( )A、 B、
B、 C、
C、 D、
D、 9. 小明用20元零花钱购买水果慰问老人,已知水果单价是每千克4元,设购买水果x千克用去的钱为y元,用图象表示y与x的函数关系,其中正确的是( )A、
9. 小明用20元零花钱购买水果慰问老人,已知水果单价是每千克4元,设购买水果x千克用去的钱为y元,用图象表示y与x的函数关系,其中正确的是( )A、 B、
B、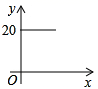 C、
C、 D、
D、 10. 某电信公司手机的收费标准有A,B两类,已知每月应缴费用 S(元)与通话时间t(分)之间的关系如图所示.当通话时间为 200 分钟时,按这两类收费标准缴费的差为( )
10. 某电信公司手机的收费标准有A,B两类,已知每月应缴费用 S(元)与通话时间t(分)之间的关系如图所示.当通话时间为 200 分钟时,按这两类收费标准缴费的差为( ) A、10 B、15 C、20 D、3011. 将 的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是 ,正方形 的顶点都在格点上,若直线 与正方形 有公共点,则 的值不可能是( )
A、10 B、15 C、20 D、3011. 将 的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是 ,正方形 的顶点都在格点上,若直线 与正方形 有公共点,则 的值不可能是( )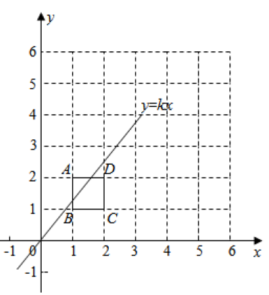 A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
12. 函数y=kx的图象经过点P(3,-1),则k的值为.13. 请你写出一个经过点(2,1)的函数解析式.14. 函数y=﹣2x+3的图象不经过第象限.15. 已知正比例函数 ,如果y的值随着x的值增大而减小,则a的取值范围是 .16. 在平面直角坐标系中,已知一次函数y=﹣ x+1的图象经过P1(x1 , y1),P2(x2 , y2)两点,若x1>x2 , 则y1y2.17. 定义[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”[1,m-2]对应的一次函数是正比例函数,则关于x的方程 的解为 .18. 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1 , l2 , l3 , ……ln分别变于点A1 , A2 , A3 , ……An;函数y=3x的图象与直线l1 , l2 , l3 , ……ln分别交于点B1 , B2 , B3 , ……Bn , 如果△OA1B1的面积记的作S1 , 四边形A1A2B2B1的面积记作S2 , 四边形A2A3B3B2的面积记作S3 , …四边形An﹣1AnBnBn﹣1的面积记作Sn , 那么S2020=.
 19. 如图,直线 交x轴于点A,交y轴于点B.以A为圆心,以AB为半径作弧交x轴于点A1;过点A1作x轴的垂线,交直线 AB于点B1 , 以A为圆心,以AB1为半径作弧交x轴于点 A2;…,如此作下去,则点 的坐标为;
19. 如图,直线 交x轴于点A,交y轴于点B.以A为圆心,以AB为半径作弧交x轴于点A1;过点A1作x轴的垂线,交直线 AB于点B1 , 以A为圆心,以AB1为半径作弧交x轴于点 A2;…,如此作下去,则点 的坐标为;
三、综合题
-
20. 已知函数y=kx+b中,自变量x的取值范围是 ,相应函数值的取值范围是 ,求该函数的表达式.21. 已知函数 .(1)、当m为何值时,y是x的一次函数?(2)、当m为何值时,y是x的正比例函数?22. 已知直线 :y=x+1和直线 :y=-2x-2相交于点P.(1)、求点P的坐标;(2)、若直线 经过点P且与直线y=3x-4平行,求直线 的函数表达式.23. 如图所示,直线 与 轴、 轴分别交于点A、B.
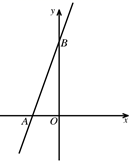 (1)、求A、B两点的坐标;(2)、求直线与两坐标轴围成的三角形的面积.
(1)、求A、B两点的坐标;(2)、求直线与两坐标轴围成的三角形的面积.