2021届高考物理二轮复习专题突破：专题二十一描述圆周运动的物理量

试卷更新日期：2021-01-25 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图所示，跷跷板转动时，跷跷板上的P、Q两点的角速度分别为 $ω_{P}$ 和 $ω_{Q}$ ，线速度大小分别为v_P和v_Q ，则（）

A、 $ω_{P}$ ＞ $ω_{Q}$ ，v_P＜v_Q B、 $ω_{P}$ = $ω_{Q}$ ，v_P=v_Q C、 $ω_{P}$ = $ω_{Q}$ ，v_P＞v_Q D、 $ω_{P}$ ＞ $ω_{Q}$ ，v_P＞v_Q

查看试题解析
2. 如图，一圆盘可绕一通过圆心且垂直于盘面的竖直轴转动，在圆盘上放一块橡皮，橡皮块随圆盘一起转动（俯视为逆时针）。物体与圆盘相对静止，某段时间圆盘转速不断减小，但仍未停止，在这段时间内，关于橡皮块所受合力F的方向的四种表示（俯视图）中，正确的是（）

A、 B、 C、 D、

查看试题解析
3. 关于圆周运动，下列说法正确的是（）

A、匀速圆周运动是匀速运动 B、匀速圆周运动是一种匀变速运动 C、圆周运动的向心加速度改变线速度的大小 D、匀速圆周运动是一种变加速运动

查看试题解析
4. 如图所示，某电视台推出了一款娱乐闯关节目，选手最容易失败落水的地方是第四关“疯狂转盘”和第五关“高空滑索”。根据所学物理知识，选出选项中表述正确的选项（）

A、选手进入转盘后，随转盘做匀速圆周运动时加速度不变 B、选手进入转盘后，在转盘中间比较安全 C、选手进入转盘后，质量越大的选手，越不容易落水 D、选手从最后一个转盘的边缘起跳去抓滑索时，起跳方向应正对悬索

查看试题解析
5. A、B两个质点均做匀速圆周运动，在相等的时间内通过的弧长之比 $s_{A} ： s_{B} = 4 ： 3$ ，转过的圆心角之比 $θ_{A} ： θ_{B} = 3 ： 2$ 。则A、B运动的（）

A、线速度之比 $v_{A} ： v_{B} = 3 ： 4$ B、角速度之比 $ω_{A} ： ω_{B} = 2 ： 3$ C、周期之比 $T_{A} ： T_{B} = 2 ： 3$ D、半径之比 $R_{A} ： R_{B} = 2 ： 1$

查看试题解析
6. 转篮球是一项需要技巧的活动，如图所示，假设某同学让篮球在指尖上匀速转动，指尖刚好静止在篮球球心的正下方。下列判断正确的是（）

A、篮球上的各点做圆周运动的圆心均在指尖与篮球的接触处 B、篮球上各点的向心力是由手指提供的 C、篮球上各点做圆周运动的角速度相等 D、篮球上各点离转轴越近，做圆周运动的向心加速度越大

查看试题解析
7. 如图所示，假设地球绕地轴自转时，在其表面上有A、B两物体(图中斜线为赤道平面)，θ₁和θ₂为已知，则（）

A、角速度之比 $ω_{A} ： ω_{B} = sin θ_{1} ： sin θ_{2}$ B、线速度之比 $v_{A} ： v_{B} = sin θ_{1} ： cos θ_{2}$ C、周期之比T_A∶T_B＝sinθ₁∶sinθ₂ D、A、B两点的向心加速度之比为 ${sin}^{2} θ_{1} ： {sin}^{2} θ_{2}$

查看试题解析
8. 如图所示为学员驾驶汽车在水平面上绕 $O$ 点做匀速圆周运动的俯视图。已知质量为60kg的学员在 $A$ 点位置，质量为70kg的教练员在 $B$ 点位置， $A$ 点的转弯半径为5.0m， $B$ 点的转弯半径为4.0m，则学员和教练员（均可视为质点）（）

A、运动周期之比为5∶4 B、运动线速度大小之比为1∶1 C、向心加速度大小之比为4∶5 D、受到的合力大小之比为15∶14

查看试题解析
9. 以下物体均在做圆周运动，运动中由摩擦力提供向心力的是（）

A、 B、 C、 D、

查看试题解析
10. 一探照灯照射在云层底面上，云层底面是与地面平行的平面，如图所示，云层底面距地面高h，探照灯以角速度ω在竖直平面内转动，当光束转到与竖直方向夹角为θ时，云层底面上光点的移动速度是（）

A、hω B、 $\frac{h ω}{c o s θ}$ C、 $\frac{h ω}{c o s^{2} θ}$ D、hωtan θ

查看试题解析
11. 有一种工作时扇面上能够显示各种图案的创意风扇，如图，其原理是在其中一片扇叶上设置一列发光二极管，当扇叶转动起来时，控制各二极管的明灭就可以显示各种图案了，如图，现令所有二极管保持同步明灭，而且每次发光均持续时间kT₂（k<1），每次灭的时间均持续（1 $-$ k）T₂ ，若扇叶转动的周期为T₁ ，且T₁、T₂、k均可在较大范围内独立调节。若在某次调试后成功显示出一个“不动”的扇环（非图所示图案），且扇环所对应的圆心角为θ，那么（）

A、k一定等于 $\frac{θ}{2 π}$ B、若重新调节，将风扇转速加倍，所看到的图案的圆心角一定变成2θ C、若重新调节，只要满足T₁>kT₂ ，所看到的图案一定为闭合的圆环 D、若重新调节，只要满足T₁=nT₂（n取1、2、3……），所看到的图案一定是“不动”的

查看试题解析
12. 某只走时准确的时钟，秒针与分针由转动轴到针尖的长度之比为3：2，则（）

A、秒针与分针的角速度之比是1：60 B、秒针针尖与分针针尖的线速度之比是90：1 C、秒针与分针针尖的向心加速度之比是3600：1 D、秒针与分针的转速之比是12：1

查看试题解析
13. 质量不计的轻质弹性杆P插在桌面上，杆端套有一个质量为m的小球，今使小球沿水平方向做半径为R的匀速圆周运动，角速度为ω，如图所示，则杆的上端受到的作用力大小为（）

A、 $m ω^{2} R$ B、 $\sqrt{m^{2} g^{2} - m^{2} ω^{4} R^{2}}$ C、 $\sqrt{m^{2} g^{2} + m^{2} ω^{4} R^{2}}$ D、不能确定

查看试题解析
14. 如图所示，一圆环以直径AB为轴做匀速转动，P、Q、R是环上的三点，则下列说法正确的是（）

A、向心加速度的大小 $a_{P} ＝ a_{Q} ＝ a_{R}$ B、任意时刻P、Q、R三点向心加速度的方向不相同 C、线速度 $v_{P} > v_{Q} > v_{R}$ D、任意时刻P、Q、R三点的线速度方向均不同

查看试题解析
15. 质量为m的小球由轻绳a和b分别系于一轻质细杆的B点和A点，如图所示，当轻杆绕轴AB以角速度ω匀速转动时，绳a与竖直方向成θ角，绳b在水平方向且长为L。小球在水平面内做匀速圆周运动，则下列说法正确的是（）

A、a绳的张力可能为零 B、a绳的张力随角速度的增大而增大 C、当角速度 $ω > \sqrt{\frac{g \tan θ}{L}}$ 时，b绳将产生弹力 D、若b绳突然被剪断，则θ一定不变

查看试题解析

二、多选题

16. 如图甲，光滑圆轨道固定在竖直面内，小球沿轨道始终做完整的圆周运动。已知小球在最低点时对轨道的压力大小为N，动能为E_k。改变小球在最低点的动能，小球对轨道压力N的大小随之改变。小球的N－E_k图线如图乙，其左端点坐标为（[1]，[2]），其延长线与坐标轴的交点分别为（0，a）、（－b，0）。重力加速度为g。则（）

A、小球的质量为 $\frac{g}{a}$ B、圆轨道的半径为 $\frac{b}{a}$ C、图乙[1]处应为5b D、图乙[2]处应为6a

查看试题解析
17. 如图所示，当用扳手拧螺母时，关于扳手上的P、Q两点的说法正确的是（）

A、P点角速度小于Q点 B、P点线速度小于Q点 C、P点向心加速度速度小于Q点 D、P点转速小于Q点

查看试题解析
18. 如图所示，为一皮带传动装置，右轮半径为r，a为它边缘上一点；左侧是一轮轴，大轮半径为4r，小轮半径为2r，b点在小轮上，到小轮中心的距离为r。c点和d点分别位于小轮和大轮的边缘上。若传动过程中皮带不打滑，则（）

A、a点和b点的角速度大小相等 B、a点和c点的线速度大小相等 C、a点和d点的向心加速度大小相等 D、abcd四点中，向心加速度最小的是a点

查看试题解析
19. 如图所示，甲､乙两水平圆盘边缘紧靠在一块，甲圆盘为主动轮，乙靠摩擦随甲转动，接触处无相对滑动｡甲圆盘与乙圆盘的半径之比为 $r_{甲} ： r_{乙} = 3 ： 1$ ；物体A距O点为 $2 r$ ，物体B距 $O^{'}$ 点为r｡在圆盘转动过程中，A和B两物体均相对圆盘静止，下列说法正确的是（）

A、物体A与B的角速度之比 $ω_{A} ： ω_{B} = 1 ： 3$ B、物体A与B的角速度之比 $ω_{A} ： ω_{B} = 3 ： 1$ C、物体A与B的线速度之比 $v_{A} ： v_{B} = 2 ： 3$ D、物体A与B的线速度之比 $v_{A} ： v_{B} = 1 ： 1$

查看试题解析
20. 如图所示，为A、B两质点做匀速圆周运动的向心加速度随半径变化的图像，其中A为双曲线的一个分支，由图可知（）．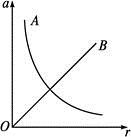

A、A物体运动的线速度大小不变 B、A物体运动的角速度大小不变 C、B物体运动的角速度大小不变 D、B物体运动的线速度大小不变

查看试题解析
21. 在马戏团表演的场地里，表演者骑在大象背上，大象绕着场地走动，若大象是沿着半径为R的圆周做匀速走动，则关于大象和表演者的受力情况，下面说法正确的是（）

A、表演者骑在大象背上不动，他受到的力是平衡力 B、表演者的向心力是地面摩擦力通过大象作用于他的 C、大象和表演者所受向心力大小与两者的质量成正比 D、大象与人两者做匀速圆周运动的向心力是地面摩擦力提供的

查看试题解析
22. 如图所示，两个相同的小球A、B用长度分别为l₁、l₂的细线（l₁<l₂）悬挂于天花板的O₁、O₂点，两球在水平面内做匀速圆周运动，两根细线与竖直轴夹角均为θ。设A、B两球的线速度分别为v_A、v_B ，角速度分别为ω_A、ω_B ，加速度分别为a_A、a_B ，两根细线的拉力分别为F_A、F_B ，则（）

A、F_A<F_B B、v_A>v_B C、a_A=a_B D、ω_A>ω_B

查看试题解析

三、填空题

23. 汽车转弯时，可认为前轮和后轮都做圆周运动，但它们的转弯半径不同，如图所示，若汽车外侧前轮的转弯半径为5m，内侧后轮的转弯半径为2.7m，若外侧前轮转弯时线速度为10m/s，则此时内侧后轮的线速度是。

查看试题解析
24. 如图所示，轮O₁、O₃固定在同一转轴上，轮O₁、O₂用皮带连接且不打滑。在O₁、O₂、O₃三个轮的边缘各取一点A、B、C，已知三个轮的半径之比r₁∶r₂∶r₃＝2∶1∶1，则：

(1)、A、B、C三点的线速度大小之比v_A∶v_B∶v_C=；

(2)、A、B、C三点的角速度大小之比ω_A∶ω_B∶ω_C=；

(3)、A、B、C三点的向心加速度大小之比a_A∶a_B∶a_C=。

查看试题解析

四、实验探究题

25. 如图，用一根结实的细绳，一端拴一个小物体．在光滑桌面上抡动细绳，使小物体做圆周运动，体验手对做圆周运动的物体的拉力．

(1)、拉力的方向是（填“沿绳指向圆心”或“垂直于绳指向速度方向”）．

(2)、增大旋转的速度，拉力将（填“变小”、“变大”或“不变”）．

(3)、松手后，小物体将沿（填“半径远离圆心”、“切线”或“半径靠近圆心”）方向运动．

查看试题解析

五、综合题

26. 在一根长为L、质量不计的细杆中点和末端各连一质量为m的小球B和C，如图所示，杆可以在竖直平面内绕固定点A转动，将杆拉到某位置放开，末端C球摆到最低位置时，杆BC段受到的拉力刚好等于C球重力的2倍．(g＝10 m/s²)求：

(1)、C球通过最低点时的线速度大小；

(2)、杆AB段此时受到的拉力大小．

查看试题解析
27. 下图1为游乐场的悬空旋转椅，可抽象为如图2所示模型，已知绳长L =5m，水平横梁L′=3m，小孩质量m=40kg，整个装置可绕竖直轴转动，绳与竖直方向夹角θ=37°，小孩可视为质点，g取10m/s² ，已知sin37°=0.6，cos37°=0.8，求：

(1)、绳子的拉力为多少？

(2)、该装置转动的角速度多大？

(3)、增大转速后，绳子与竖直方向的夹角变为53°，求此时装置转动的角速度。

查看试题解析
28. 如图所示，一轻杆一端固定在转轴O上，在距O点为杆长的 $\frac{2}{5}$ 处固定一小球，轻杆以角速度ω绕O点在竖直平面内匀速转动。在杆转过的圆心角为θ的时间内，杆的端点通过的弧长为s，求：

(1)、小球的线速度大小；

(2)、小球的向心加速度大小。

查看试题解析

2021届高考物理二轮复习专题突破：专题二十一 描述圆周运动的物理量

一、单选题

二、多选题

三、填空题

四、实验探究题

五、综合题

2021届高考物理二轮复习专题突破：专题二十一描述圆周运动的物理量