江西省宜春一中2020-2021学年高一上学期数学第一次月考试卷
试卷更新日期:2021-01-25 类型:月考试卷
一、单选题
-
1. 下列四组对象中能构成集合的是( ).A、本校学习好的学生 B、在数轴上与原点非常近的点 C、很小的实数 D、倒数等于本身的数2. 已知 ,则 的值为( )A、15 B、7 C、31 D、173. 集合 的另一种表示法是( )A、 B、 C、 D、4. 给出下列关系:
①12∈R;②2∈Q;③|﹣3|∈N;④|-3|∈Z;⑤0∉N,其中正确的个数为( )
A、1 B、2 C、3 D、45. 若函数 是幂函数,且图像与坐标轴无交点,则 ( )A、是偶函数 B、是奇函数 C、是单调递减函数 D、在定义域内有最小值6. 下列各组函数中,f(x)与g(x)相等的是( )A、 , B、 , C、 , D、 ,7. 如图,阴影部分用集合 、 、 表示为( ) A、 B、 C、 D、8. 已知函数 的定义域为 ,则函数 的定义域为( )A、 B、 C、 D、9. 函数 的图象大致为( )A、
A、 B、 C、 D、8. 已知函数 的定义域为 ,则函数 的定义域为( )A、 B、 C、 D、9. 函数 的图象大致为( )A、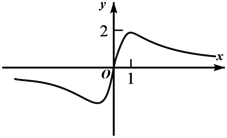 B、
B、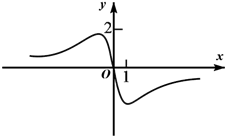 C、
C、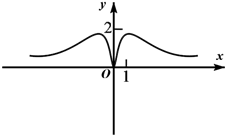 D、
D、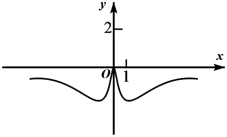 10. 已知函数 ,若f(x)在(-∞,+∞)上是增函数,则实数a的取值范围是( )A、(12,1] B、(12,+∞) C、[1,+∞) D、[1,2]11. 已知奇函数y=f(x)在定义域(﹣1,1)上是减函数,且f(2a﹣1)+f(a﹣1)<0,则实数a的取值范围是( )A、(0,+∞) B、(0,2) C、( ,1) D、( ,+∞)12. 当一个非空数集G满足“如果a,b∈G,则a+b,a﹣b,ab∈G,且b≠0时, ”时,我们称G就是一个数域,以下四个关于数域的命题:
10. 已知函数 ,若f(x)在(-∞,+∞)上是增函数,则实数a的取值范围是( )A、(12,1] B、(12,+∞) C、[1,+∞) D、[1,2]11. 已知奇函数y=f(x)在定义域(﹣1,1)上是减函数,且f(2a﹣1)+f(a﹣1)<0,则实数a的取值范围是( )A、(0,+∞) B、(0,2) C、( ,1) D、( ,+∞)12. 当一个非空数集G满足“如果a,b∈G,则a+b,a﹣b,ab∈G,且b≠0时, ”时,我们称G就是一个数域,以下四个关于数域的命题:①0是任何数域的元素;②若数域G有非零元素,则2017∈G;③集合P={x|x=2k,k∈Z}是一个数域;④有理数集是一个数域.其中正确的有( )
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 已知集合 ,且 ,则实数m的值为.14. 函数f(x)=-x2+3x-2的单调增区间是 .15. 若函数f(x)满足3f(x)﹣f( )=x2 , 则f(2)= .16. 设函数f(x)=x|x|+b,给出四个命题:
①y=f(x)是偶函数;
②f(x)是实数集R上的增函数;
③b=0,函数f(x)的图象关于原点对称;
④函数f(x)有两个零点.
命题正确的有 .
三、解答题
-
17. 已知集合 .(1)、若 ,求实数 的取值范围;(2)、若 是单元素集,求 的值及集合 .18. 求下列函数的值域.(1)、 ,x∈[3,5];(2)、 .19. 已知集合 或 , ,(1)、求 , ;(2)、若 ,求实数 的取值范围.20. 已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0.(1)、判断函数f(x)的奇偶性,并给出证明;(2)、求证:函数f(x)是R上的减函数.