人教版数学七年级下册 第五章 相交线与平行线 5.3.1 平行线的性质 同步练习
试卷更新日期：2021-01-24 类型：同步测试
一、单选题
-
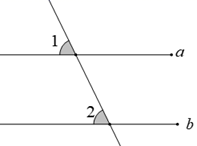
1. 如图，直线a，b被直线c所截，且a//b，若∠1=55°，则∠2等于（ ）
A、35° B、45° C、55° D、125°2. 如图，A点在B点的北偏东40°方向，C点在B点的北偏东75°方向，A点在C点的北偏西50°方向，则∠BAC的度数是（ ）
A、85° B、80° C、90° D、95°3. 如图，直线 ，且 于点 ，若 ，则 的度数为（ ）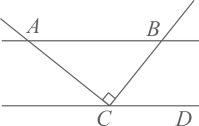
A、65° B、55° C、45° D、35°4. 如图，将一副三角板按如图所示的方式摆放，其中两条斜边 ， 角的顶点与含 角的直角三角板的直角顶点重合，点E，D，C在同一条直线上，则 的为（ ）
A、 B、 C、 D、5. 将一把直尺和一块含 角的直角三角板按如图所示方式摆放，其中 ， .若 ，则 的度数为（ ）
A、 B、 C、 D、6. 如图， ， ，则 ， ， 之间的关系是（ ）
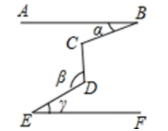A、 B、 C、 D、7. 如图，将一副三角板和一张对边平行的纸条按如图方式摆放两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是（ ）
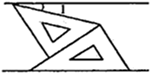A、30° B、25° C、20° D、15°8. 如图，AB∥EF，∠ABP＝ ∠ABC，∠EFP＝ ∠EFC，已知∠FCD＝60°，则∠P的度数为（ ）
A、60° B、80° C、90° D、100°9. 如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE=α，∠DCE=β．下列各式：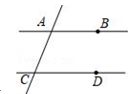
①α+β，②α﹣β，③β﹣α，④360°﹣α﹣β，∠AEC的度数可能是（ ）
A、①②③ B、①②④ C、①③④ D、①②③④ 图4二、填空题
-
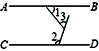
10. 如图，AB∥CD，∠1=50°，∠2=110°，则∠3=度．
11. 如图，AB∥CD∥EF，若∠A=30°，∠AFC=15°，则∠C=.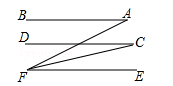
12. 如图，AB∥CD.EF⊥AB于E，EF交CD于F，已知∠1＝58°，则∠2＝.
13. 如图，将一副三角板和一张对边平行的纸条按如图方式摆放，则∠α的度数是.
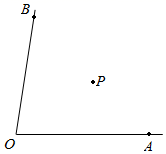
14. 已知∠A与∠B（ ， ）的两边-边平行，另一边互相垂直，且 ，则∠A的度数为°.15. 问题情境：如图1，已知
， 
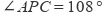.求 
的度数.
(1)、经过思考，小敏的思路是：如图2，过P作
，根据平行线有关性质，可得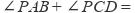 
. (2)、问题迁移：如图3，
，点P在射线OM上运动， 
， 
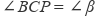. ①当点P在A，B两点之间运动时，
、 
、 
之间有何数量关系？请说明理由.②如果点P在A，B两点外侧运动时（点P与点A，B，O三点不重合），请你直接写出
、 、 之间的数量关系，(3)、问题拓展：如图4，
， 
是一条折线段，依据此图所含信息，把你所发现的结论，用简洁的数学式子表达为. 三、解答题
-
16. 如图，有三个论断① ；② ；③ ，请从中任选两个作为条件，另一个作为结论构成一个命题，并证明该命题的正确性．
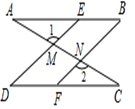17. 如图所示，点E在AB上，CE，DE分别平分∠BCD，∠ADC，∠1+∠2＝90°，∠B＝75°，求∠A的度数．
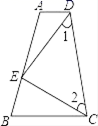18. 如图，B处在A处南偏西50°方向，C处在A处的南偏东20°方向，C处在B处的北偏东80°方向，求∠ACB的度数.
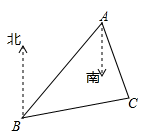19. 如图 ，AB∥CD，且∠PMQ=2∠QMB，∠PNQ=2∠QND，判断∠P 与∠Q的数量关系，并说明理由．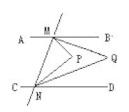
四、作图题
