人教版数学七年级下册 第五章 相交线与平行线 5.1.2 垂线 同步练习
试卷更新日期：2021-01-24 类型：同步测试
一、单选题
-
1. 若线段 ， 分别是 边上的高线和中线，则（ ）A、 B、 C、 D、2. 如图，连接直线 外一点 与直线 上各点 ， ，其中 ，这些线段 ， ， ， ， 中，最短的线段是（ ）
A、 B、 C、 D、3. 如图，AC⊥BC，AC=4.5，若点P在直线BC上，则AP的长可能是（ ）.
A、5 B、4 C、3 D、24. 如图，把河 中的水引到村庄C拟修水渠中最短的是（ ）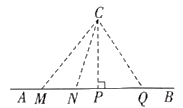
A、 B、 C、 D、5. 如图，在平面内作已知直线m的垂线，可作垂线的条数有（ ）
A、0条 B、1条 C、2条 D、无数条6. 如图，直线 ， 相交于点O， ，垂足为点O.若 ，则 的度数为（ ）
A、 B、 C、 D、7. 在同－平面内，若∠A与∠B的两边分别垂直，且∠A比∠B的3倍少40°，则∠A的度数为（ ）A、20° B、55° C、20°或 125° D、20°或55°8. 如图，点O为直线AB上一点，OC⊥OD. 如果∠1=35°，那么∠2的度数是（ ）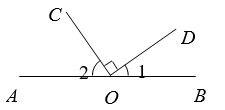
A、35° B、45° C、55° D、65°9. 如图所示，∠BAC=90°，AD⊥BC，则下列结论中，正确的个数为（ ）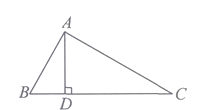
①AB⊥AC； ②AD与AC互相垂直； ③点C到AB的垂线段是线段AB；
④点A到BC的距离是线段AD的长度； ⑤线段AB的长度是点B到AC的距离；
⑥AD+BD>AB．
A、2个 B、3个 C、4个 D、5个10. 如图所示，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（ ）
①∠AOB＝∠COD；②∠AOB＋∠COD＝90°；③∠BOC＋∠AOD＝180°；④∠AOC－∠COD＝∠BOC.
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
11. 如图，某单位要在河岸 上建一个水泵房引水到C处，他们的做法是：过点C作 于点D，将水泵房建在了D处．这样做最节省水管长度，其数学道理是 ．
12. 如图，在Rt . ，在边 、 上分别截取 ， ，使 ，分别以D、E为圆心，以大于 的长为半径作弧，两弧在 内交于点M，作射线 交 边于点F．若 ，则点F到 的距离为 ．
13. 如图，线段AB=15cm ， 线段AD=12cm ， 线段AC=9cm ， 则点A到BC的距离为 cm ．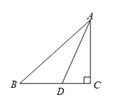
14. 如图，CD⊥AB，垂足是点D，AC＝7，BC＝5，CD＝4，点E是线段AB上的一个动点（包括端点），连接CE，那么CE长的范围是 ．
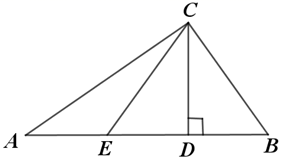15. 已知 的两边与∠B的两边分别垂直，且 比∠B的3倍少 ，那么16. 如图，已知 .若 ，则 ．
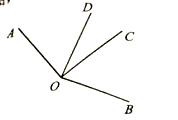17. 如图，将一副直角三角板放在同一条直线AB上，其中∠ONM=30°，∠OCD=45°．将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周，在旋转的过程中，当第秒时，直线CD恰好与直线MN垂直．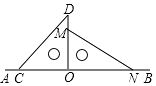
三、解答题
-
18. 如图，直线AB、CD相交于点O，EO⊥AB，垂足为O，∠EOC：∠AOD=7：11，求∠DOE的度数.
19. 如图，直线AB与CD相交于点O，EO⊥CD于点O，OF平分∠AOD，且∠BOE＝50°.求∠COF的度数．
