天津市静海区2020-2021学年高三上学期数学第一次月考试卷

试卷更新日期：2021-01-22 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知全集 $U = {- 1 ， 0 ， 1 ， 2 ， 3}$ ，集合 $A = {0 ， 1 ， 2}$ ， $B = {- 1 ， 0 ， 1}$ ，则 $(∁_{U} A) \cap B =$ （）

A、{-1} B、 ${0 ， 1}$ C、 ${- 1 ， 2 ， 3}$ D、 ${- 1 ， 0 ， 1 ， 3}$

查看试题解析
2. 设命题 $p ： \exists x \in R$ ， $2^{x} > 2012$ ，则 $\neg P$ 为（）．

A、 $\forall x \in R$ ， $2^{x} \leq 2012$ B、 $\forall x \in R$ ， $2^{x} > 2012$ C、 $\exists x \in R$ ， $2^{x} \leq 2012$ D、 $\exists x \in R$ ， $2^{x} < 2012$

查看试题解析
3. 函数 $y = (x^{3} - x) 2^{| x |}$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
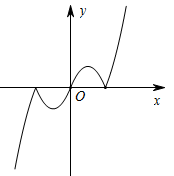4. 学校为了解学生在课外读物方面的支出情况，抽取了n位同学进行调查，结果显示这些同学的支出都在 $[10 ， 50]$ ，（单位：元）之间，其频率分布直方图如图所示，其中支出在 $[10 ， 30)$ （单位：元）内的同学有33人，则支出在 $[40 ， 50]$ （单位：元）内的同学人数为（）

A、100 B、120 C、30 D、300

查看试题解析
5. 若棱长为2的正方体的顶点都在同一球面上，则该球的表面积为（）

A、12π B、24π C、36π D、144π

查看试题解析
6. 已知 $a > b$ ，则下列成立的是（）

A、 $\sqrt{a} > \sqrt{b}$ B、 $a^{2} > b^{2}$ C、 $\frac{a}{c^{2}} > \frac{b}{c^{2}}$ D、 $a c^{2} > b c^{2}$

查看试题解析
7. 若双曲线过点 $(3 ， \sqrt{2})$ ，且渐近线方程为 $y = \pm \frac{1}{3} x$ ，则该双曲线的方程是（）．

A、 $y^{2} - \frac{x^{2}}{9} = 1$ B、 $\frac{y^{2}}{9} - x^{2} = 1$ C、 $x^{2} - \frac{y^{2}}{9} = 1$ D、 $\frac{x^{2}}{9} - y^{2} = 1$

查看试题解析
8. 设 $a = \log_{2} π$ ， $b = \log_{\frac{1}{2}} π$ ， $c = π^{- 2}$ ，则（）

A、 $a > b > c$ B、 $b > a > c$ C、 $a > c > b$ D、 $c > b > a$

查看试题解析
9. 已知函数 $f (x) = {\begin{array}{l} a^{x} ， x > 1 \\ (4 - \frac{a}{2}) x + 2 ， x \leq 1 \end{array}$ 是 $R$ 上的单调递增函数，则实数 $a$ 的取值范围是（）

A、 $(1 ， + \infty)$ B、 $[4 ， 8)$ C、 $(4 ， 8)$ D、 $(1 ， 8)$

查看试题解析

二、填空题

10. i是虚数单位，计算 $\frac{1 - 2 i}{2 + i}$ 的结果为．

查看试题解析
11. 在 ${(2 x - \frac{1}{\sqrt{x}})}^{5}$ 的展开式中，含 $x^{2}$ 的系数为.

查看试题解析
12. 从3名男生和2名女生中随机选取两人，则两人恰好是一名男生和一名女生的概率是．

查看试题解析
13. 已知圆C的圆心在x轴的正半轴上，点 $M (0 ， \sqrt{5})$ 在圆C上，且圆心到直线 $2 x - y = 0$ 的距离为 $\frac{4 \sqrt{5}}{5}$ ，则圆C的方程为.

查看试题解析
14. 已知 $a > 0$ ， $b > 0$ 且 $2 a + b = a b$ ，则a+2b的最小值为．

查看试题解析
15. 若不等式 $k x^{2} - 6 k x + k + 8 \geq 0$ 对任意 $x \in R$ 恒成立，则实数 $k$ 的取值范围为.

查看试题解析

三、解答题

16. 已知函数 $f (x) = \sqrt{3} \cos 2 x + \sin 2 x + 1$
（I）求 $f (x)$ 的最小正周期及对称轴方程；

（Ⅱ）求 $f (x)$ 在区间 $[0 ， \frac{π}{2}]$ 上的最值．

查看试题解析
17. 在 $Δ A B C$ 中，内角 $A$ ， $B$ ， $C$ 所对的边分别是 $a$ ， $b$ ， $c$ ．已知 $a = 2$ ， $c = \sqrt{2}$ ， $cos A = - \frac{\sqrt{2}}{4}$ ．
（Ⅰ）求 $\sin C$ 和 $b$ 的值；

（Ⅱ）求 $\cos (2 A + \frac{π}{3})$ 的值．

查看试题解析
18. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E为 $B B_{1}$ 的中点．

（Ⅰ）求证： $B C_{1} / /$ 平面 $A D_{1} E$ ；

（Ⅱ）求直线 $A A_{1}$ 与平面 $A D_{1} E$ 所成角的正弦值．

查看试题解析
19. 已知 ${a_{n}}$ 是各项均为正数的等比数列， ${b_{n}}$ 是等差数列，且 $a_{1} = b_{1} = 1$ ， $b_{2} + b_{3} = 2 a_{3}$ ， $a_{5} - 3 b_{2} = 7$ ．

(1)、求 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、 $c_{n} = a_{n} b_{n}$ ， $n \in N^{*}$ 求数列 ${c_{n}}$ 的前n项和．

查看试题解析
20. 已知函数 $f (x) = x^{2} + 2 a \ln x .$

(1)、若函数 $f (x)$ 的图象在 $(2 ， f (2))$ 处的切线斜率为l，求实数 $a$ 的值；

(2)、求函数 $f (x)$ 的单调区间.

查看试题解析