四川省绵阳市江油市八校联考2020-2021学年七年级上学期数学12月月考试卷
试卷更新日期:2021-01-21 类型:月考试卷
一、单选题
-
1. 有下列各数:3,+(-2.6), - ,0,-|-2|,其中正数有( )A、1个 B、2个 C、3个 D、4个2. 下列运算正确的是( )A、a+2a2=3a3 B、2a+b=2ab C、4a-a=3 D、3a2b-2ba2=a2 b3. 2019年2月5日《流浪地球》上映,这部由刘慧欣小说《流浪地球》改编的同名电影,5天累计票房达到了16亿元,成为名副其实的首部国产科幻大片,数据16亿用科学记数法表示为( ).A、 B、 C、 D、4. 下列立体图形中,从正面看,看到的图形是三角形的是( )A、
 B、
B、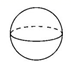 C、
C、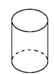 D、
D、 5. 下列说法中正确的个数是( )
5. 下列说法中正确的个数是( )⑴ 表示负数;
⑵多项式 的次数是3;
⑶单项式 的系数为 ;
⑷若 ,则 .
A、0个 B、1个 C、2个 D、3个6. 方程 去分母得( )A、 B、 C、 D、7. 下列说法:①任何有理数都可以用数轴上的点表示;②|-5|与-(-5)互为相反数;③m+1一定比m大;④近似数1.21×104精确到百分位.其中正确的有( )A、4个 B、3个 C、2个 D、1个8. 某商场购进一批服装,每件进价为1000元,由于换季滞销,商场决定将这种服装重新标价后按标价的7折销售.若想打折后每件服装仍能获利5%,该服装的标价应是( )A、1500元 B、1400元 C、1300元 D、1200元9. 如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠AOM=35°,则∠CON的度数为( )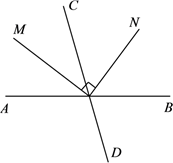 A、35° B、45° C、55° D、65°10. 如图,数轴上 两点对应的数分别是 和 .对于以下四个式子:① ;② ;③ ;④ ,其中值为负数的是( )
A、35° B、45° C、55° D、65°10. 如图,数轴上 两点对应的数分别是 和 .对于以下四个式子:① ;② ;③ ;④ ,其中值为负数的是( ) A、①② B、③④ C、①③ D、②④
A、①② B、③④ C、①③ D、②④二、填空题
-
11. 在算式5-|-8□2|中的“□”里,填入运算符号 , 使得算式的值最大(在符号“+,-,×,÷”中选择一个).12. 单项式 - 的系数是 ,次数是13. 若角α是锐角,则角α的补角比角α的余角大度.14. 方程3x+20=4x-25的解为.15. 如图,在数轴上有A,B,C,D四个点,且2AB=BC=3CD,若A,D两点表示的数分别为-5,6,点E为BD的中点,则该数轴上点E表示的数是.
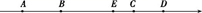 16. 已知 和 互为相反数,那么 等于 .17. 众所周知,中华诗词博大精深,集大量的情景、情感于短短数十字之间,或豪放,或婉约,或思民生疾苦,或抒发己身豪情逸致,文化价值极高.而数学与古诗词更是有着密切的联系.古诗中,五言绝句是四句诗,每句都是五个字;七言绝句是四句诗,每句都是七个字.有一本诗集,其中五言绝句比七言绝句多13首,总字数反而少了20个字.根据题意可知七言绝句有首.18. 将一张长方形纸片按如图5所示的方式折叠,BC、BD为折痕,则∠CBD为度.
16. 已知 和 互为相反数,那么 等于 .17. 众所周知,中华诗词博大精深,集大量的情景、情感于短短数十字之间,或豪放,或婉约,或思民生疾苦,或抒发己身豪情逸致,文化价值极高.而数学与古诗词更是有着密切的联系.古诗中,五言绝句是四句诗,每句都是五个字;七言绝句是四句诗,每句都是七个字.有一本诗集,其中五言绝句比七言绝句多13首,总字数反而少了20个字.根据题意可知七言绝句有首.18. 将一张长方形纸片按如图5所示的方式折叠,BC、BD为折痕,则∠CBD为度. 19. 一组“数值转换机”按图所示的程序计算,如果输入的数是30,则输出结果为56,要使输出结果为60,则输入的正整数是 .
19. 一组“数值转换机”按图所示的程序计算,如果输入的数是30,则输出结果为56,要使输出结果为60,则输入的正整数是 . 20. 如果∠AOB=34°,∠BOC=18°,那么∠AOC的度数是.
20. 如果∠AOB=34°,∠BOC=18°,那么∠AOC的度数是.三、解答题
-
21. 计算:(1)、 ;(2)、6×( - )-32÷(-12).22. 化简并求值:3(x2-2xy)-(- xy+ )+(x2-2y2),其中x、y取值的位置如图所示.
 23. 先画图,再解答:(1)、画线段AB,并反向延长AB到点C,使AC= AB,再取BC的中点D;(2)、若线段CD=6cm,求线段AB的长.24. 如图,已知 为直线 上一点,过点 向直线 上方引三条射线 、 、 ,且 平分 , .
23. 先画图,再解答:(1)、画线段AB,并反向延长AB到点C,使AC= AB,再取BC的中点D;(2)、若线段CD=6cm,求线段AB的长.24. 如图,已知 为直线 上一点,过点 向直线 上方引三条射线 、 、 ,且 平分 , . (1)、若 °,求 的度数;(2)、若 °,求 的度数;25. 关于x的方程2(x﹣3)﹣m=2的解和方程3x﹣7=2x的解相同.(1)、求m的值;(2)、已知线段AB=m,在直线AB上取一点P,恰好使AP=2PB,点Q为PB的中点,求线段AQ的长.
(1)、若 °,求 的度数;(2)、若 °,求 的度数;25. 关于x的方程2(x﹣3)﹣m=2的解和方程3x﹣7=2x的解相同.(1)、求m的值;(2)、已知线段AB=m,在直线AB上取一点P,恰好使AP=2PB,点Q为PB的中点,求线段AQ的长. 26. 滴滴快车是一种便捷的出行工具,计价规则如下表:
26. 滴滴快车是一种便捷的出行工具,计价规则如下表:计费项目
里程费
时长费
远途费
单价
1.8元/公里
0.45元/分钟
0.4元/公里
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.4元.
(1)、若小东乘坐滴滴快车,行车里程为20公里,行车时间为30分钟,则需付车费元.(2)、若小明乘坐滴滴快车,行车里程为a公里,行车时间为b分钟,则小明应付车费多少元(用含a、b的代数式表示,并化简.)(3)、小王与小张各自乘坐滴滴快车,行车里程分别为9.5公里与14.5公里,如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差多少分钟?27. 如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.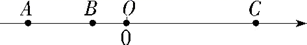 (1)、写出数轴上点A、C表示的数;(2)、点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN= CQ.设运动的时间为t(t>0)秒.
(1)、写出数轴上点A、C表示的数;(2)、点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN= CQ.设运动的时间为t(t>0)秒.①求数轴上点M、N表示的数(用含t的式子表示);
②t为何值时,M、N两点到原点的距离相等?
28. 如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.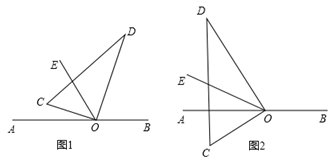 (1)、如图1,若∠COE=20°,则∠BOD=;若∠COE=α,则∠BOD=(用含α的代数式表示);(2)、将图1中三角板绕O逆时针旋转到图2的位置时,试猜测∠COE与∠BOD之间有怎样的数量关系,并说明理由.
(1)、如图1,若∠COE=20°,则∠BOD=;若∠COE=α,则∠BOD=(用含α的代数式表示);(2)、将图1中三角板绕O逆时针旋转到图2的位置时,试猜测∠COE与∠BOD之间有怎样的数量关系,并说明理由.