湖南省长沙市周南教育集团2020-2021学年七年级上学期数学12月月考试卷
试卷更新日期:2021-01-21 类型:月考试卷
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下面各组线段中,能组成三角形的是( )A、6,9,14 B、8,8,16 C、10,5,4 D、5,11,63. 点 关于 轴对称的点 的坐标是( )A、 B、 C、 D、4. 下面四个图形中,线段BD是△ABC的高的是( )A、
2. 下面各组线段中,能组成三角形的是( )A、6,9,14 B、8,8,16 C、10,5,4 D、5,11,63. 点 关于 轴对称的点 的坐标是( )A、 B、 C、 D、4. 下面四个图形中,线段BD是△ABC的高的是( )A、 B、
B、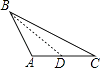 C、
C、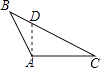 D、
D、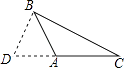 5. 过多边形的一个顶点可以引出6条对角线,则多边形的边数是( )A、7 B、8 C、9 D、106. 下列各式从左到右的变形中,是因式分解的是( )A、 B、 C、 D、7. 下列条件中,能利用“ ”判定△ ≌△A′B′C′的是 ( )A、AB=A′B′,AC=A′C′,∠C=∠C′ B、AB=A′B′,∠A=∠A′,BC=B′C′ C、AC=A′C′,∠C=∠C′,BC=B′C′ D、AC=A′C′,∠A=∠A′,BC=B′C′8. 如图用尺规作∠A′O′B′=∠AOB的依据是( )
5. 过多边形的一个顶点可以引出6条对角线,则多边形的边数是( )A、7 B、8 C、9 D、106. 下列各式从左到右的变形中,是因式分解的是( )A、 B、 C、 D、7. 下列条件中,能利用“ ”判定△ ≌△A′B′C′的是 ( )A、AB=A′B′,AC=A′C′,∠C=∠C′ B、AB=A′B′,∠A=∠A′,BC=B′C′ C、AC=A′C′,∠C=∠C′,BC=B′C′ D、AC=A′C′,∠A=∠A′,BC=B′C′8. 如图用尺规作∠A′O′B′=∠AOB的依据是( ) A、SAS B、ASA C、AAS D、SSS9. 如果 是一个完全平方式,那么m的值是( )A、7 B、-7 C、-5或7 D、-5或510. 在元旦联欢会上,三个小朋友分别站在三角形的三个顶点的位置上,他们玩抢凳子游戏,要求在他们中间放一个木凳,谁先做到凳子上谁就获胜,为使游戏公平,则凳子应放在三角形的( )A、三条角平分线的交点 B、三条中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点11. 若有理数a、b满足|a+3|+(b﹣2)2=0,则代数式 的值为( )A、9 B、6 C、﹣9 D、-612. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,BF平分∠ABC,过点C作CF⊥BF于F点,过A作AD⊥BF于D点.AC与BF交于E点,下列四个结论:①BE=2CF;②AD=DF;③AD+DE= BE;④AB+BC=2AE.其中正确结论的序号是( )
A、SAS B、ASA C、AAS D、SSS9. 如果 是一个完全平方式,那么m的值是( )A、7 B、-7 C、-5或7 D、-5或510. 在元旦联欢会上,三个小朋友分别站在三角形的三个顶点的位置上,他们玩抢凳子游戏,要求在他们中间放一个木凳,谁先做到凳子上谁就获胜,为使游戏公平,则凳子应放在三角形的( )A、三条角平分线的交点 B、三条中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点11. 若有理数a、b满足|a+3|+(b﹣2)2=0,则代数式 的值为( )A、9 B、6 C、﹣9 D、-612. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,BF平分∠ABC,过点C作CF⊥BF于F点,过A作AD⊥BF于D点.AC与BF交于E点,下列四个结论:①BE=2CF;②AD=DF;③AD+DE= BE;④AB+BC=2AE.其中正确结论的序号是( ) A、只有①②③ B、只有②③ C、只有①②④ D、只有①④
A、只有①②③ B、只有②③ C、只有①②④ D、只有①④二、填空题
-
13. 计算: .14. 正五边形的内角和等于度.15. 分解因式: .16. 如图,在等边△ABC中, 于点D,若 ,则 .
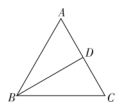 17. 如图,一架梯子斜靠在墙上,梯子与地面的夹角∠B=60°,梯子与墙角的距离BC为3m,则梯子的长AB为m.
17. 如图,一架梯子斜靠在墙上,梯子与地面的夹角∠B=60°,梯子与墙角的距离BC为3m,则梯子的长AB为m. 18. 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”,他的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了 ( 为非负整数)的展开式中 按次数从大到小排列的项的系数,例如: 展开式中的系数1,2,1恰好对应图中第三行的数字; 展开式中的系数1,3,3,1恰好对应图中第四行的数字…….请认真观察此图,根据前面各式的规律,写出 的展开式: .
18. 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”,他的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了 ( 为非负整数)的展开式中 按次数从大到小排列的项的系数,例如: 展开式中的系数1,2,1恰好对应图中第三行的数字; 展开式中的系数1,3,3,1恰好对应图中第四行的数字…….请认真观察此图,根据前面各式的规律,写出 的展开式: .
三、解答题
-
19. 如图点 , , , ,在同一条直线上,点 , 在直线 的两侧, 平行于 , 平行于 , ,求证: .
 20. 先化简,再求值.
20. 先化简,再求值.(2x+3y)-2-(2x+3y)(2x-3y),其中x=-2,y= .
21. 如图,已知 各顶点的坐标分别为 , , .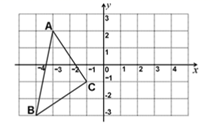 (1)、请你画出 关于 轴对称的 ,(2)、并写出 的各点坐标;(3)、求 的面积;22. 在 中, , 平分 交 于点 , 垂直平分线段 .
(1)、请你画出 关于 轴对称的 ,(2)、并写出 的各点坐标;(3)、求 的面积;22. 在 中, , 平分 交 于点 , 垂直平分线段 . (1)、求 ;(2)、若 , ,求 的长.23. 如图,△ABC中,AB=AC,∠B的平分线交AC于D,E是BD延长线上的一点,且AE=AC.
(1)、求 ;(2)、若 , ,求 的长.23. 如图,△ABC中,AB=AC,∠B的平分线交AC于D,E是BD延长线上的一点,且AE=AC. (1)、求证:AE//BC;(2)、若AD=DC=2,求BC的长.24. 如图, , , , 、 交于点 ,连接 .
(1)、求证:AE//BC;(2)、若AD=DC=2,求BC的长.24. 如图, , , , 、 交于点 ,连接 . (1)、求证: ;(2)、求证: 平分 .25. 好学的小东同学,在学习多项式乘以多项式时发现: 的结果是一个多项式,并且最高次项为: ,常数项为: ,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是: ,即一次项为 .
(1)、求证: ;(2)、求证: 平分 .25. 好学的小东同学,在学习多项式乘以多项式时发现: 的结果是一个多项式,并且最高次项为: ,常数项为: ,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是: ,即一次项为 .请你认真领会小东同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)、计算 所得多项式的一次项系数为 .(2)、若计算 所得多项式不含一次项,求 的值;(3)、若 ,则 .26. 如图,已知 中, , ,点 为 的中点. (1)、如果点 在线段 上以 的速度由 点向 点运动,同时点 在线段 上由 向 点运动.
(1)、如果点 在线段 上以 的速度由 点向 点运动,同时点 在线段 上由 向 点运动.①若点 的运动速度与点 的运动速度相等,经过1秒后, 与 是否全等,请说明理由;
②若点 的运动速度与点 的运动速度不相等,当点 的运动速度为多少时,能够使 与 全等?
(2)、若点 以②中的运动速度从点 出发,点 以原来的运动速度从点 同时出发,都逆时针沿 三边运动,求经过多长时间点 与点 第一次在 的哪条边上相遇?