湖南省长沙市雅礼集团2020-2021学年七年级上学期数学第二次月考试卷
试卷更新日期:2021-01-21 类型:月考试卷
一、单选题
-
1. 计算 的结果等于( )A、 B、 C、 D、2. 习近平总书记提出了未来五年“精准扶贫”的战略构想,意味着每年要减贫约11700000人,将数据11700000用科学记数法表示为( )A、1.17×107 B、11.7×106 C、0.117×107 D、1.17×1083. 下列四个几何体中,左视图为圆的是( )A、
 B、
B、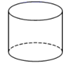 C、
C、 D、
D、 4. 若 , ,且 ,则式子a+b的值是( )A、7 B、1 C、1或-1 D、7或-75. 若关于 、 的多项式 中没有二次项,则 ( )A、3 B、2 C、 D、6. 已知 ,则代数式 的值是( )A、2 B、-2 C、-4 D、7. 下列方程变形正确的是( )A、由3+x=5,得x=5+3 B、由3=x-2,得x=3+2 C、由 y=0,得y=2 D、由7x=-4,得x=-8. 点M在线段AB上,给出下列四个条件,其中不能判定点M是线段AB中点的是( )A、AM=BM B、AB=2AM C、BM= AB D、AM+BM=AB9. 轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )A、 B、 C、 D、10. 某车间有34名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮和3个小齿轮配成一套,问分别安排多少名工人加工大小齿轮,才能刚好配套?若设加工大齿轮的工人有x名,则可列方程为( )A、3×10x=2×16(34-x) B、3×16x=2×10(34-x) C、2×16x=3×10(34-x) D、2×10x=3×16(34-x)11. 如图,已知点 将线段 分成 的两部分,点 是 的中点,若 ,则线段 的长为( ).
4. 若 , ,且 ,则式子a+b的值是( )A、7 B、1 C、1或-1 D、7或-75. 若关于 、 的多项式 中没有二次项,则 ( )A、3 B、2 C、 D、6. 已知 ,则代数式 的值是( )A、2 B、-2 C、-4 D、7. 下列方程变形正确的是( )A、由3+x=5,得x=5+3 B、由3=x-2,得x=3+2 C、由 y=0,得y=2 D、由7x=-4,得x=-8. 点M在线段AB上,给出下列四个条件,其中不能判定点M是线段AB中点的是( )A、AM=BM B、AB=2AM C、BM= AB D、AM+BM=AB9. 轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )A、 B、 C、 D、10. 某车间有34名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮和3个小齿轮配成一套,问分别安排多少名工人加工大小齿轮,才能刚好配套?若设加工大齿轮的工人有x名,则可列方程为( )A、3×10x=2×16(34-x) B、3×16x=2×10(34-x) C、2×16x=3×10(34-x) D、2×10x=3×16(34-x)11. 如图,已知点 将线段 分成 的两部分,点 是 的中点,若 ,则线段 的长为( ).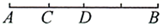 A、6 B、8 C、10 D、1212. 阅读:关于x方程ax=b在不同的条件下解的情况如下:(1)当a≠0时,有唯一解x= ;(2)当a=0,b=0时有无数解;(3)当a=0,b≠0时无解.请你根据以上知识作答:已知关于x的方程 •a= - (x-6)无解,则a的值是( )A、1 B、-1 C、±1 D、a≠1
A、6 B、8 C、10 D、1212. 阅读:关于x方程ax=b在不同的条件下解的情况如下:(1)当a≠0时,有唯一解x= ;(2)当a=0,b=0时有无数解;(3)当a=0,b≠0时无解.请你根据以上知识作答:已知关于x的方程 •a= - (x-6)无解,则a的值是( )A、1 B、-1 C、±1 D、a≠1二、填空题
-
13. 的相反数是.14. 已知x=2是方程2x+m-4=0的一个根,则m的值为 .15. 若 , 互为相反数, , 互为倒数, 是最大的负整数,则 .16. 某书店把一本新书按标价的八折出售,仍获利30%,若该书的进价为40元,则标价为元.17. 已知线段AB=16 cm,直线AB上有一点C,且BC=10 cm,M是线段AC的中点,则AM的长为 cm.18. 有理数a、b、c在数轴上的位置如图所示,则化简 得到的结果是 。
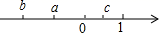
三、解答题
-
19. 计算:(1)、(2)、20. 计算(1)、(2)、21. 已知(1)、若 ,求 的值(2)、若 的值与 的值无关,求 的值22. 马虎同学在解方程 时,不小心把等式左边m前面的“-”当做“+”进行求解,得到的结果为x=1,求代数式m2-2m+1的值.23. 某城市自来水收费实行阶梯水价,收费标准如下表所示:
月用水量
不超过12吨的部分
超过12吨的部分且
不超过18吨的部分
超过18吨的部分
收费标准
2元/吨
2.5元/吨
3元/吨
(1)、某用户四月份用水量为16吨,需交水费为多少元?(2)、某用户五月份交水费50元,所用水量为多少吨?(3)、某用户六月份用水量为a吨,需要交水费为多少元?24. 如图,点 在线段 上,点 分别是 的中点.(1)、若 ,求线段MN 的长;(2)、若 为线段 上任一点,满足 ,其它条件不变,你能求出 的长度吗?请说明理由.(3)、若 在线段 的延长线上,且满足 分别为 AC、BC的中点,你能求出 的长度吗?请画出图形,写出你的结论,并说明理由. 25. 在数轴上,对于不重合的三点 , , ,给出如下定义:
25. 在数轴上,对于不重合的三点 , , ,给出如下定义:若点 到点 的距离是点 到点 的距离的2倍,我们就把点 叫做 的新冠点.
例如:如图,点 表示的数为-1,点 表示的数为2.表示数1的点 到点 的距离是2,到点 的距离是1.那么点 是 的新冠点;又如,表示数0的点 到点 的距离是1,到点 的距离是2,那么点 就不是 的新冠点,但点 是 的新冠点.
 (1)、当点 表示的数为-4,点 表示的数为8时,若点 表示的数为4,则点 (填“是”或“不是”) 的新冠点.(2)、当点 表示的数为-4,点 表示的数为8时,若点 是 的新冠点,求点 表示的数.(3)、若 , 在数轴上表示的数分别为-2和4,现有一点 从点 出发,以每秒1个单位长度的速度向数轴负半轴方向运动,当点 到达点 时停止.问点 运动多少秒时, , , 中恰有一个点为其余两点的新冠点.26. 已知:如下图,点 是线段 上一定点, , 、 两点分别从 、 出发以 、 的速度沿直线 向左同时运动,运动方向如箭头所示( 在线段 上, 在线段 上)
(1)、当点 表示的数为-4,点 表示的数为8时,若点 表示的数为4,则点 (填“是”或“不是”) 的新冠点.(2)、当点 表示的数为-4,点 表示的数为8时,若点 是 的新冠点,求点 表示的数.(3)、若 , 在数轴上表示的数分别为-2和4,现有一点 从点 出发,以每秒1个单位长度的速度向数轴负半轴方向运动,当点 到达点 时停止.问点 运动多少秒时, , , 中恰有一个点为其余两点的新冠点.26. 已知:如下图,点 是线段 上一定点, , 、 两点分别从 、 出发以 、 的速度沿直线 向左同时运动,运动方向如箭头所示( 在线段 上, 在线段 上) (1)、若 ,当点 、 运动了 ,此时 , ;(直接填空)(2)、若点 、 运动时,总有 ,求 的值.(3)、在(2)的条件下, 是直线 上一点,且 ,求 的值.
(1)、若 ,当点 、 运动了 ,此时 , ;(直接填空)(2)、若点 、 运动时,总有 ,求 的值.(3)、在(2)的条件下, 是直线 上一点,且 ,求 的值.