山东省日照市2020-2021学年九年级上学期数学第二次月考试卷

试卷更新日期：2021-01-21 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各式不能确定为反比例函数关系的是（）

A、 $x y = 3$ B、 $y = - 3 x^{- 1}$ C、 $y = \frac{3}{2 x}$ D、 $y = \frac{k}{x}$

查看试题解析
2. 下列四张扑克牌图案，属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 对于双曲线y= $\frac{1 - m}{x}$ ，当x>0时，y随x的增大而减小，则m的取值范围为（）

A、m>0 B、m>1 C、m<0 D、m<1

查看试题解析
4. 将抛物线 $y = - 2 x^{2} - 3$ 向右平移2个单位长度，再向上平移1个单位长度，得到的抛物线解析式为（）

A、 $y = - 2 {(x + 2)}^{2} + 2$ B、 $y = - 2 {(x - 2)}^{2} - 2$ C、 $y = - 2 {(x + 2)}^{2} - 2$ D、 $y = - 2 {(x - 2)}^{2} - 5$

查看试题解析
5. 若一个圆锥的侧面积是底面积的2倍，则圆锥侧面展开图的扇形的圆心角为（　　）

A、120° B、180° C、240° D、300°

查看试题解析
6. 在一个不透明的袋子里装有3个白球，1个黑球，这些球除颜色外其余都相同，从中随机摸出一个球，记下颜色后放回，搅匀后再随机摸出一个球，则两次摸出的球是一白一黑的概率为（）

A、 $\frac{3}{16}$ B、 $\frac{1}{4}$ C、 $\frac{3}{8}$ D、 $\frac{1}{2}$

查看试题解析
7. 已知点 $A (- 1, y_{1})$ ， $B (1, y_{2})$ ， $C (2, y_{3})$ 是函数 $y = - \frac{1}{x}$ 图象上的三点，则 $y_{1}, y_{2}, y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{3} < y_{1}$ C、 $y_{3} < y_{2} < y_{1}$ D、无法确定

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A = 90 °$ ， $\sin B = \frac{1}{3}$ ， $A C = 2$ ，则 $B C$ 的长为（）

A、2 B、4 C、6 D、8

查看试题解析
9. 如图，正比例函数 $y = a x$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象相交于 $A$ ， $B$ 两点，其中点 $A$ 的横坐标为2，则不等式 $a x < \frac{k}{x}$ 的解集为（）

A、 $x < - 2$ 或 $x > 2$ B、 $x < - 2$ 或 $0 < x < 2$ C、 $- 2 < x < 0$ 或 $0 < x < 2$ D、 $- 2 < x < 0$ 或 $x > 2$

查看试题解析
10.
在平行四边形ABCD中，点E是边AD上一点，且AE=2ED，EC交对角线BD于点F，则 $\frac{E F}{F C}$ 等于（　　）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
11.
如图，点A是反比例函数y= $\frac{k}{x}$ 的图象上的一点，过点A作AB⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC的面积为3，则k的值是（　　）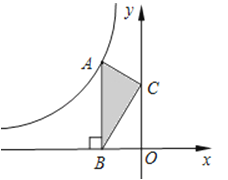

A、3 B、﹣3 C、6 D、﹣6

查看试题解析
12. 如图，若二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象的对称轴为直线 $x = 1$ ，与y轴交于点C，与x轴交于点A，点 $B (- 1 ， 0)$ ，则：① $a + b > a m^{2} + b m (m \neq 1)$ ；② $a b c > 0$ ；③ $b^{2} - 4 a c > 0$ ；④当 $y > 0$ 时， $- 1 < x < 3$ ；⑤ $3 a + c = 0$ ．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 在平面直角坐标系中， $△$ ABC和 $△$ A₁B₁C₁的相似比等于 $\frac{1}{3}$ ，并且是关于原点O的位似图形，若点A的坐标为(3，6)，则其对应点A₁的坐标是

查看试题解析
14. 如图，已知 $A$ 是双曲线 $y = \frac{2}{x} (x > 0)$ 上一点，过点 $A$ 作 $A B / / y$ 轴，交双曲线 $y = - \frac{1}{x} (x > 0)$ 于点 $B$ ，过点 $B$ 作 $B C ⊥ A B$ 交 $y$ 轴于点 $C$ ．连接 $A C$ ，则 $△ A B C$ 的面积为．

查看试题解析
15. 如图，正方形EFGH内接于 $△ A B C$ ，AD⊥BC于点D，交EH于点M，BC＝10cm，AD＝20cm．则正方形EFGH的边长是．

查看试题解析
16. 如图，∠A＝∠B＝90°，AB＝7，AD＝2，BC＝3，在边AB上取点P，使得△PAD与△PBC相似，则满足条件的AP长.

查看试题解析

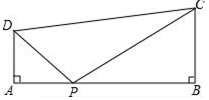
三、解答题

17. 计算

(1)、 $2 \sin 30^{\circ} + \cos 60^{\circ} - \tan 60^{\circ} • \tan 30^{\circ} + \cos^{2} 45^{\circ}$

(2)、 $\sqrt{16} + {(- \frac{1}{2})}^{- 1} + {(\sqrt{3} - 5)}^{0} - \sqrt{3} \cos 30^{\circ}$

查看试题解析
18.
媒体报道，近期“手足口病”可能进入发病高峰期，某校根据《学校卫生工作条例》，为预防“手足口病”，对教室进行“薰药消毒”．已知药物在燃烧及释放过程中，室内空气中每立方米含药量y（毫克）与燃烧时间x（分钟）之间的关系如图所示（即图中线段OA和双曲线在A点及其右侧的部分），根据图象所示信息，解答下列问题：

(1)、写出从药物释放开始，y与x之间的函数关系式及自变量的取值范围

(2)、据测定，当空气中每立方米的含药量低于2毫克时，对人体无毒害作用，那么从消毒开始，至少在多长时间内，师生不能进入教室？

查看试题解析
19. 如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙上的影高为2米，求旗杆的高度．

查看试题解析
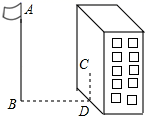20. 某书店销售儿童书刊，一天可出售20套，每套盈利40元．为了扩大销售，增加盈利，尽快减少库存，书店决定采取降价措施．若一套书每降价1元，平均每天可多出售2套．

(1)、若要书店每天盈利1200元，则需降价多少元？

(2)、设书店一天可获利润y元，当每套书降价多少元时，书店可获最大利润？最大利润为多少？

查看试题解析
21. 如图，Rt△ABC中，∠ABC＝90°，以AB为直径的⊙O交AC于点D，E是BC的中点连接DE、OE．

(1)、试判断DE与⊙O的位置关系，并说明理由；

(2)、若⊙O半径r＝6，DE＝8，求AD的长．

查看试题解析
22. 如图，抛物线 $y = x^{2} - 2 x - 3$ 与x轴交于A、B两点（A点在B点左侧），直线l与抛物线交于A、C两点，其中C点的横坐标为2．

(1)、求A、B两点的坐标及直线AC的函数表达式；

(2)、P是线段AC上的一个动点，设点P横坐标是m，过P点作y轴的平行线交抛物线于E点，请用含m的代数式表示线段PE长度，并求出PE的最大长度；

(3)、若点G是抛物线上的动点，点F是x轴上的动点，判断有几个位置能使点A、C、F、G为顶点的四边形是平行四边形，写出点F的坐标．

查看试题解析