湖南省长沙市周南教育集团2020-2021学年九年级上学期数学12月月考试卷
试卷更新日期:2021-01-21 类型:月考试卷
一、单选题
-
1. 的绝对值为( )A、 B、2 C、 D、2. 若二次根式 有意义,则 x 的取值范围是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 若反比例函数y= (k≠0)的图象经过点(2,﹣1),则这个函数的图象一定经过点( )A、( ,﹣2) B、(1,2) C、(﹣1, ) D、(1,﹣2)5. 已知等腰三角形的两边长分别为 ,则该三角形的周长为( )A、 B、 C、 或 D、 或6. 如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )
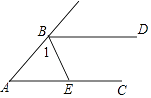 A、65° B、60° C、55° D、50°7. 一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )
A、65° B、60° C、55° D、50°7. 一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )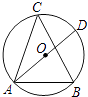 A、 B、 C、 D、8. 将抛物线 向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为( )A、 B、 C、 D、9. 在平行四边形 中,若 ,则 的度数是( )A、50° B、60° C、70° D、80°10. 一元二次方程x2﹣2x+m=0总有实数根,则m应满足的条件是( )A、m>1 B、m=1 C、m<1 D、m≤111. 如图是二次函数y=﹣x2+2x+4的图象,使y≤1成立的x的取值范围是( )
A、 B、 C、 D、8. 将抛物线 向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为( )A、 B、 C、 D、9. 在平行四边形 中,若 ,则 的度数是( )A、50° B、60° C、70° D、80°10. 一元二次方程x2﹣2x+m=0总有实数根,则m应满足的条件是( )A、m>1 B、m=1 C、m<1 D、m≤111. 如图是二次函数y=﹣x2+2x+4的图象,使y≤1成立的x的取值范围是( ) A、-1 ≤ x ≤ 3 B、x ≤-1 C、x ≥ 1 D、x ≤-1或x ≥ 312. 《九章算术》是我国古代内容极为丰富的数学名著.书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是“今有直角三角形(如图),勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
A、-1 ≤ x ≤ 3 B、x ≤-1 C、x ≥ 1 D、x ≤-1或x ≥ 312. 《九章算术》是我国古代内容极为丰富的数学名著.书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是“今有直角三角形(如图),勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )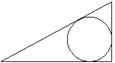 A、3步 B、5步 C、6步 D、8步
A、3步 B、5步 C、6步 D、8步二、填空题
-
13. 同时抛掷三枚质地均匀的硬币,三枚硬币全部正面向上的概率是 .14. 关于x的反比例函数 ( 为常数),当x>0时, 随 的增大而减小,则m的取值范围为 .15. 如图所示,将一个含 角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是度.
 16. 如图所示,将边长为 的正方形 沿直线 向右滚动(不滑动),当正方形滚动两周时(当正方形的四个顶点的位置首次与起始位置相同时,称为正方形滚动一周),正方形的顶点 所经过的路线长是 .
16. 如图所示,将边长为 的正方形 沿直线 向右滚动(不滑动),当正方形滚动两周时(当正方形的四个顶点的位置首次与起始位置相同时,称为正方形滚动一周),正方形的顶点 所经过的路线长是 .
三、解答题
-
17. 计算:18. 先化简,再求值: ,其中 .19. 如图,在 中, ,将 绕点 顺时针旋转60°,得到 ,连接 交 于点 ,回答下列问题:
 (1)、 是什么三角形: .(2)、求 与 的周长之和是多少?20. 为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部对 四个厂家的同型号的零件共2000件进行合格率检测,通过检测得出 厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.
(1)、 是什么三角形: .(2)、求 与 的周长之和是多少?20. 为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部对 四个厂家的同型号的零件共2000件进行合格率检测,通过检测得出 厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图. (1)、扇形统计图中 厂家对应的圆心角为;(2)、抽查 厂家的合格零件为件,并将图1补充完整;(3)、若要从 四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树形图的方法求出 两个厂家同时被选中的概率.21. 下图中曲线是反比例函数 的图象的一支.
(1)、扇形统计图中 厂家对应的圆心角为;(2)、抽查 厂家的合格零件为件,并将图1补充完整;(3)、若要从 四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树形图的方法求出 两个厂家同时被选中的概率.21. 下图中曲线是反比例函数 的图象的一支. (1)、这个反比例函数图象的另一支位于哪个象限?常数 的取值范围是什么?(2)、若一次函数 的图象与反比例函数图象交于点 ,与 轴交于点 的面积为2,求 的值.22. 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知 .
(1)、这个反比例函数图象的另一支位于哪个象限?常数 的取值范围是什么?(2)、若一次函数 的图象与反比例函数图象交于点 ,与 轴交于点 的面积为2,求 的值.22. 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知 . (1)、作出 以 为旋转中心,顺时针旋转90°的 ,(只画出图形).(2)、作出 关于原点 成中心对称的 ,(只画出图形)(3)、在(1)的条件下,求出线段 扫过的面积.23. 如图,AB是⊙O的直径,点C,D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA的延长线与OC的延长线于点E,F,连接BF.
(1)、作出 以 为旋转中心,顺时针旋转90°的 ,(只画出图形).(2)、作出 关于原点 成中心对称的 ,(只画出图形)(3)、在(1)的条件下,求出线段 扫过的面积.23. 如图,AB是⊙O的直径,点C,D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA的延长线与OC的延长线于点E,F,连接BF. (1)、求证:BF是⊙O的切线;(2)、已知⊙O的半径为2,求EF的长.24. 已知 是关于 的函数,若其图像经过点 ,则称点 为函数图象上的“偏离点”.例如:直线 上存在“偏离点” .(1)、在双曲线 上是否存在“偏离点”?若存在,请求出“偏离点”的坐标;若不存在,请说明理由.(2)、若抛物线 上有“偏离点”,且“偏离点”为 和 ,求 的最小值(用含 的式子表示);(3)、若函数 的图像上存在唯一的一个“偏离点”,且当 时, 的最小值为 ,求 的值.25. 定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形 中,若 , ,则称四边形 为准平行四边形.
(1)、求证:BF是⊙O的切线;(2)、已知⊙O的半径为2,求EF的长.24. 已知 是关于 的函数,若其图像经过点 ,则称点 为函数图象上的“偏离点”.例如:直线 上存在“偏离点” .(1)、在双曲线 上是否存在“偏离点”?若存在,请求出“偏离点”的坐标;若不存在,请说明理由.(2)、若抛物线 上有“偏离点”,且“偏离点”为 和 ,求 的最小值(用含 的式子表示);(3)、若函数 的图像上存在唯一的一个“偏离点”,且当 时, 的最小值为 ,求 的值.25. 定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形 中,若 , ,则称四边形 为准平行四边形.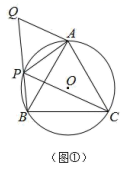

 (1)、如(图①), 、 、 、 是⊙O上的四个点, ,延长 到 ,使 .求证:四边形 是准平行四边形;(2)、如(图②),准平行四边形 内接于⊙O, , ,若⊙O的半径为5, ,求 的长;(3)、如(图③),在 中, , , ,若四边形 是准平行四边形,且 ,请直接写出 长的最大值.
(1)、如(图①), 、 、 、 是⊙O上的四个点, ,延长 到 ,使 .求证:四边形 是准平行四边形;(2)、如(图②),准平行四边形 内接于⊙O, , ,若⊙O的半径为5, ,求 的长;(3)、如(图③),在 中, , , ,若四边形 是准平行四边形,且 ,请直接写出 长的最大值.