湖南省长沙市长郡教育集团2020-2021学年九年级上学期数学第三次月考试卷
试卷更新日期:2021-01-21 类型:月考试卷
一、单选题
-
1. 在实数 ,-3.14,0, , 中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 8月上映的战争题材影片《八佰》取材自“八百壮士”奉命坚守上海四行仓库的真实历史,呈现出平凡的中国军民共同奋勇抗战的热血情怀.截止10月17日,累计票房达到了30.81亿,登顶2020年度票房全球冠军.其中,30.81亿用科学记数法表示为( )A、 B、 C、 D、3. 点M(3, )与Q(a,b)关于y轴对称,则a+b的值为( )A、1 B、 C、5 D、4. 下列说法:①若一个数的倒数等于它本身,则这个数是1或-1;②若2a2与3ax+1的和是单项式,则x=1;③若|x|=|-7|,则x=-7;④若a,b互为相反数,则a,b的商为-1.其中正确的个数为( )A、1 B、2 C、3 D、45. 一种饮料有两种包装,2大盒、4小盒共装88瓶,3大盒、2小盒共装84瓶,大盒与小盒每盒各装多少瓶?设大盒装x瓶,小盒装y瓶,则可列方程组( )A、 B、 C、 D、6. 抛物线 ,下列说法正确的是( )A、开口向下,顶点坐标(2,3) B、开口向上,顶点坐标(2, ) C、开口向下,顶点坐标( ,3) D、开口向上,顶点坐标(2, 3 )7. 如图,转盘中四个扇形的面积都相等.小明随意转动转盘1次,指针指向的数字为偶数的概率为( )
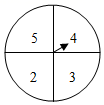 A、 B、 C、 D、8. 已知抛物线 与x轴没有交点,则函数 的大致图象是( )A、
A、 B、 C、 D、8. 已知抛物线 与x轴没有交点,则函数 的大致图象是( )A、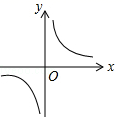 B、
B、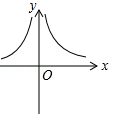 C、
C、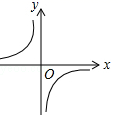 D、
D、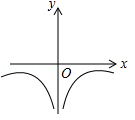 9. 如图,点E是 的边 上的一点,且 ,连接 并延长交 的延长线于点F,若 ,则 的周长为( )
9. 如图,点E是 的边 上的一点,且 ,连接 并延长交 的延长线于点F,若 ,则 的周长为( )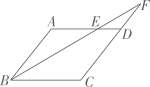 A、21 B、28 C、34 D、4210. 如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(2,4).点A在 轴的正半轴上,点C在 轴的正半轴上,点P是BC的中点.以坐标原点O为位似中心,将矩形OABC放大为原图形的1.5倍,记点P的对应点为P1 , 则P1的坐标为( )
A、21 B、28 C、34 D、4210. 如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(2,4).点A在 轴的正半轴上,点C在 轴的正半轴上,点P是BC的中点.以坐标原点O为位似中心,将矩形OABC放大为原图形的1.5倍,记点P的对应点为P1 , 则P1的坐标为( )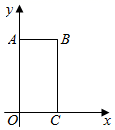 A、(3,3) B、(3,2)或( , ) C、(3,3)或( , ) D、(2,3)或( , )11. 如图,在地面上的点A处测得树顶B的仰角为 ,AC=2,则树高BC为(用含 的代数式表示)( )
A、(3,3) B、(3,2)或( , ) C、(3,3)或( , ) D、(2,3)或( , )11. 如图,在地面上的点A处测得树顶B的仰角为 ,AC=2,则树高BC为(用含 的代数式表示)( ) A、 B、 C、 D、12. 如图,直线y= x+1与x轴、y轴分别相交于A、B两点,P是该直线上的任一点,过点D(3,0)向以P为圆心, AB为半径的⊙P作两条切线,切点分别为E、F,则四边形PEDF面积的最小值为( )
A、 B、 C、 D、12. 如图,直线y= x+1与x轴、y轴分别相交于A、B两点,P是该直线上的任一点,过点D(3,0)向以P为圆心, AB为半径的⊙P作两条切线,切点分别为E、F,则四边形PEDF面积的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 小明用 计算一组数据的方差,那么 .14. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=cm.
 15. 如图,第一象限内的点A在反比例函数y= 上,第二象限的点B在反比例函数y= 上,且OA⊥OB, ,BC、AD垂直于x轴于C、D,则k的值为 .
15. 如图,第一象限内的点A在反比例函数y= 上,第二象限的点B在反比例函数y= 上,且OA⊥OB, ,BC、AD垂直于x轴于C、D,则k的值为 .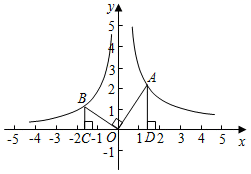 16. 如图,在矩形ABCD中,BC=6,AB=2,Rt△BEF的顶点E在边CD或延长线上运动,且∠BEF=90°,EF= BE,DF= ,则BE= .
16. 如图,在矩形ABCD中,BC=6,AB=2,Rt△BEF的顶点E在边CD或延长线上运动,且∠BEF=90°,EF= BE,DF= ,则BE= .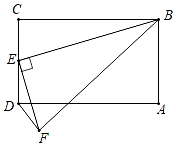
三、解答题
-
17. 计算: .18. 先化简,再求值: ,其中 满足方程 .19. 解不等式组: 并把解集在数轴上表示出来.
 20. 某校组织八年级部分学生开展庆“五·四”演讲比赛,赛后对全体参赛学生成绩按A、B、C、D四个等级进行整理,得到下列不完整的统计图表.
20. 某校组织八年级部分学生开展庆“五·四”演讲比赛,赛后对全体参赛学生成绩按A、B、C、D四个等级进行整理,得到下列不完整的统计图表.
等级
频数
频率
A
4
0.08
B
20
a
C
b
0.3
D
11
0.22
请根据所给信息,解答下列问题:
(1)、参加此次演讲比赛的学生共有人,a= , b= .(2)、请计算扇形统计图中B等级对应的扇形的圆心角的度数;(3)、已知A等级四名同学中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加县级比赛,请用列表法或树状图,求甲、乙两名同学都被选中的概率.21. 为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山。汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶。已知BC=80千米,∠A=45°,∠B=30°。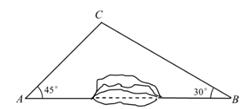 (1)、开通隧道前,汽车从A地到B地大约要走多少千米?(2)、开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据: ≈1.41, ≈1.73)22. 如图,在平面直角坐标系 中,直线 与双曲线 ( )相交于点A、B,已知点B(a, ),点C在 轴正半轴上,点D(2, ),连接OA,OD,DC,AC,四边形AODC为菱形.
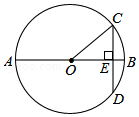
(1)、开通隧道前,汽车从A地到B地大约要走多少千米?(2)、开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据: ≈1.41, ≈1.73)22. 如图,在平面直角坐标系 中,直线 与双曲线 ( )相交于点A、B,已知点B(a, ),点C在 轴正半轴上,点D(2, ),连接OA,OD,DC,AC,四边形AODC为菱形.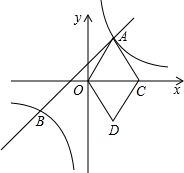 (1)、求k和m的值;(2)、请直接写出:当 取何值时,反比例函数值大于一次函数值?(3)、设P是 轴上一动点,且△OAP的面积等于菱形OACD的面积,求点P的坐标.23. 如图,已知以 的边 为直径作 的外接圆的 平分线 交 于D,交 于 ,过E作 交 的延长线于F.
(1)、求k和m的值;(2)、请直接写出:当 取何值时,反比例函数值大于一次函数值?(3)、设P是 轴上一动点,且△OAP的面积等于菱形OACD的面积,求点P的坐标.23. 如图,已知以 的边 为直径作 的外接圆的 平分线 交 于D,交 于 ,过E作 交 的延长线于F.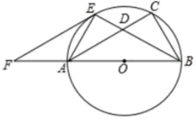 (1)、求证: 是 切线;(2)、若 求 的长.24. 定义:若一次函数 与反比例函数 同时经过点P( , )则称二次函数 为一次函数与反比例函数的“关联函数”,称点P为关联点.例如:一次函数 与反比例函数 ,都经过(2,4),则 就是两个函数的“关联函数”.(1)、判断 与 是否存在“关联函数”,如果存在,请求出“关联点”和相应“关联函数”.如果不存在,请说明理由;(2)、已知:整数a,b,c满足条件 ,并且一次函数 与反比例函数 存在“关联函数” ,求a的值.(3)、若一次函数 和反比例函数 在自变量 的值满足 的情况下.其“关联函数”的最小值为6,求其“关联函数”的解析式.25. 在平面直角坐标系中,抛物线 ( )与 轴的两个交点分别为A、B,与 轴相交于点C,点A( ,0), ,连接BC,tan∠OCB=2.
(1)、求证: 是 切线;(2)、若 求 的长.24. 定义:若一次函数 与反比例函数 同时经过点P( , )则称二次函数 为一次函数与反比例函数的“关联函数”,称点P为关联点.例如:一次函数 与反比例函数 ,都经过(2,4),则 就是两个函数的“关联函数”.(1)、判断 与 是否存在“关联函数”,如果存在,请求出“关联点”和相应“关联函数”.如果不存在,请说明理由;(2)、已知:整数a,b,c满足条件 ,并且一次函数 与反比例函数 存在“关联函数” ,求a的值.(3)、若一次函数 和反比例函数 在自变量 的值满足 的情况下.其“关联函数”的最小值为6,求其“关联函数”的解析式.25. 在平面直角坐标系中,抛物线 ( )与 轴的两个交点分别为A、B,与 轴相交于点C,点A( ,0), ,连接BC,tan∠OCB=2. (1)、求该抛物线的解析式;(2)、设点P是抛物线上在第一象限内的动点(不与C、B重合),过点P做PD⊥BC,垂足为点D.
(1)、求该抛物线的解析式;(2)、设点P是抛物线上在第一象限内的动点(不与C、B重合),过点P做PD⊥BC,垂足为点D.①点P在运动过程中,线段PD的长度是否存在最大值?若存在,请求出点D的坐标;若不存在,请说明理由;
②以P、D、C为顶点的三角形与△COA相似时,求出点P的坐标.