四川省绵阳市江油市2020-2021学年八年级上学期数学12月月考试卷
试卷更新日期:2021-01-21 类型:月考试卷
一、单选题
-
1. 在长为10cm , 7cm , 5cm , 3cm的四根木条,选其中三根组成三角形,则能组成三角形的个数为( )A、1 B、2 C、3 D、42. 在下列图形中是轴对称图形的是( )A、
 B、
B、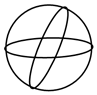 C、
C、 D、
D、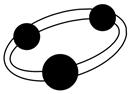 3. 下列因式分解正确的是( )A、 B、 C、 D、4. 已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )A、90° B、110° C、100° D、120°5. 已知,点 与点 关于 轴对称,则 的值为( )A、 B、1 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,AD平分∠BAC,AB=AC,连接BD,CD并延长,分别交AC,AB于点F,E,则图中全等三角形共有( )
3. 下列因式分解正确的是( )A、 B、 C、 D、4. 已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )A、90° B、110° C、100° D、120°5. 已知,点 与点 关于 轴对称,则 的值为( )A、 B、1 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,AD平分∠BAC,AB=AC,连接BD,CD并延长,分别交AC,AB于点F,E,则图中全等三角形共有( ) A、2对 B、3对 C、4对 D、5对8. 已知 , ,则 的值为( ).A、 B、 C、 D、9. 为提高市民的环保意识,某市发出“节能减排,绿色出行”的倡导,某企业抓住机遇投资20万元购买并投放一批 型“共享单车”,因为单车需求量增加,计划继续投放 型单车, 型单车的投放数量与 型单车的投放数量相同,投资总费用减少 ,购买 型单车的单价比购买 型单车的单价少50元,则 型单车每辆车的价格是多少元?设 型单车每辆车的价格为 元,根据题意,列方程正确的是( )A、 B、 C、 D、10. 如图,在等腰△ABC与等腰△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α,连接BD和CE相交于点P,交AC于点M,交AD与点N.下列结论:①BD=CE;②∠BPE=180∘−2α;③AP平分∠BPE;④若α=60∘,则PE=AP+PD.其中一定正确的结论的个数是( )
A、2对 B、3对 C、4对 D、5对8. 已知 , ,则 的值为( ).A、 B、 C、 D、9. 为提高市民的环保意识,某市发出“节能减排,绿色出行”的倡导,某企业抓住机遇投资20万元购买并投放一批 型“共享单车”,因为单车需求量增加,计划继续投放 型单车, 型单车的投放数量与 型单车的投放数量相同,投资总费用减少 ,购买 型单车的单价比购买 型单车的单价少50元,则 型单车每辆车的价格是多少元?设 型单车每辆车的价格为 元,根据题意,列方程正确的是( )A、 B、 C、 D、10. 如图,在等腰△ABC与等腰△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α,连接BD和CE相交于点P,交AC于点M,交AD与点N.下列结论:①BD=CE;②∠BPE=180∘−2α;③AP平分∠BPE;④若α=60∘,则PE=AP+PD.其中一定正确的结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
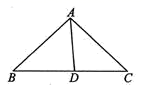
11. 一个正多边形的每个外角为60°,那么这个正多边形的内角和是。12. 分解因式:x4﹣16=.13. 石墨烯目前是世界上最薄、最坚硬的纳米材料,其理论厚度仅0.00000000034米,这个数用科学记数法表示为 .14. 如图,在△ABC中,AB=AC,D为BC上一点,且CD=AD ,AB=BD,则∠B的度数为 .
 15. 如图,在△ABC和△DEF中,已知CB=DF,∠C=∠D,要使△ABC≌△EFD,还需添加一个条件,那么这个条件可以是 .
15. 如图,在△ABC和△DEF中,已知CB=DF,∠C=∠D,要使△ABC≌△EFD,还需添加一个条件,那么这个条件可以是 . 16. 如图,△ABC中,BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC= .
16. 如图,△ABC中,BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC= . 17. 已知 是完全平方式,则 .18. 若分式方程 =a 无解,则a的值为.
17. 已知 是完全平方式,则 .18. 若分式方程 =a 无解,则a的值为.三、解答题
-
19. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
 20. 解分式方程: ﹣1= .21. 如图,在平面直角坐标系中, 的三个顶点分别为 .
20. 解分式方程: ﹣1= .21. 如图,在平面直角坐标系中, 的三个顶点分别为 .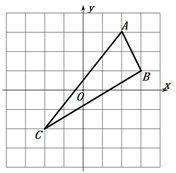 (1)、请在图中作出 关于 轴的对称图形 ( 的对称点分别是 ) ,并直接写出 的坐标;(2)、求 的面积22. 正在建设的“汉十高铁”竣工通车后,若襄阳至武汉段路程与当前动车行驶的路程相等,约为325千米,且高铁行驶的速度是当前动车行驶速度的2.5倍,则从襄阳到武汉乘坐高铁比动车所用时间少1.5小时.求高铁的速度.
(1)、请在图中作出 关于 轴的对称图形 ( 的对称点分别是 ) ,并直接写出 的坐标;(2)、求 的面积22. 正在建设的“汉十高铁”竣工通车后,若襄阳至武汉段路程与当前动车行驶的路程相等,约为325千米,且高铁行驶的速度是当前动车行驶速度的2.5倍,则从襄阳到武汉乘坐高铁比动车所用时间少1.5小时.求高铁的速度.
23. 如图,已知DE⊥AE,垂足为E,DF⊥AC,垂足为F,BD=CD,BE=CF. (1)、求证:AD平分∠BAC;(2)、丁丁同学观察图形后得出结论:AB+AC=2AE,请你帮他写出证明过程.24. 在等边 中,线段 为 边上的中线.动点 在直线 上时,以 为一边在 的下方作等边 ,连结BE.(1)、若点 在线段 上时(如图),则 (填“>”、“<”或“=”), 度;
(1)、求证:AD平分∠BAC;(2)、丁丁同学观察图形后得出结论:AB+AC=2AE,请你帮他写出证明过程.24. 在等边 中,线段 为 边上的中线.动点 在直线 上时,以 为一边在 的下方作等边 ,连结BE.(1)、若点 在线段 上时(如图),则 (填“>”、“<”或“=”), 度;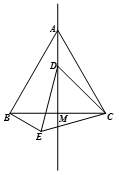 (2)、设直线BE与直线 的交点为O.
(2)、设直线BE与直线 的交点为O.①当动点 在线段 的延长线上时(如图),试判断 与 的数量关系,并说明理由;
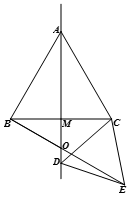
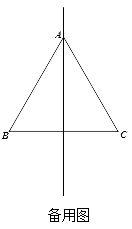
②当动点 在直线 上时,试判断 是否为定值?若是,请直接写出 的度数;若不是,请说明理由.
25. 如图,已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.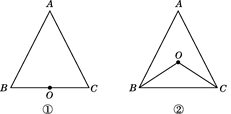 (1)、如图①,若点O在BC上,求证:△ABC是等腰三角形.(2)、如图②,若点O在△ABC内部,求证AB=AC.(3)、若点O在△ABC的外部,AB=AC还成立吗?请画图说明.
(1)、如图①,若点O在BC上,求证:△ABC是等腰三角形.(2)、如图②,若点O在△ABC内部,求证AB=AC.(3)、若点O在△ABC的外部,AB=AC还成立吗?请画图说明.