山东省微山县2020-2021学年八年级上学期数学第三次月考试卷

试卷更新日期：2021-01-21 类型：月考试卷

进入 出卷网 下载

一、单选题

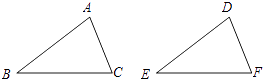
  • 1. 下列长度的三条线段，哪一组不能构成三角形（ ）
    A、3，3，3 B、3，4，5 C、5，6，10 D、4，5，9

    查看试题解析

  • 2. 点P（－2，3）关于y轴对称的点的坐标是（  ）
    A、（2，3） B、（－2，3） C、（2，－3） D、（－2，－3）

    查看试题解析

  • 3. 下列运算正确的是（  ）
    A、x4+x4=x8 B、x6÷x2=x3 C、x•x4=x5 D、（x2）3=x8

    查看试题解析

  • 4. 若3x=10，3y=5，则3x+y的值是（  ）
    A、15 B、50 C、0.5 D、2

    查看试题解析

  • 5. 一个等腰三角形的两边长分别是3和7，则它的周长为（  ）
    A、17 B、15 C、13 D、13或17

    查看试题解析

  • 6. 如图，给出下列四组条件：

    ①AB=DE，BC=EF，AC=DF；

    ②AB=DE，∠B=∠E．BC=EF；

    ③∠B=∠E，BC=EF，∠C=∠F；

    ④AB=DE，AC=DF，∠B=∠E．

    其中，能使△ABC≌△DEF的条件共有（  ）

    A、1组 B、2组 C、3组 D、4组

    查看试题解析

  • 7. 如图，在△ABC中，AB＝AC，且D为BC上一点，CD＝AD，AB＝BD，则∠B的度数为（  ）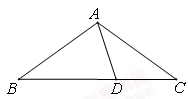

    A、30° B、36° C、40° D、45°

    查看试题解析

  • 8. 如图，在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R、S，若AQ＝PQ，PR＝PS，①PA平分∠BAC；②AS＝AR；③QP∥AR；④△BRP≌△CSP．则这四个结论中正确的有（ ）

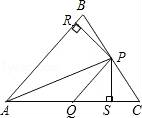    A、4个 B、3个 C、2个 D、1个

    查看试题解析

  • 9. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图所示）就是一例．

    这个三角形的构造法则为：两腰上的数都是1，其余每个数均为其上方左右两数之和．事实上，这个三角形给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）2=a2+2ab+b2展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）3=a3+3a2b+3ab2+b3展开式中各项的系数等等．根据上面的规律，请你猜想（a+b）7的展开式中所有系数的和是（  ）

    A、2018 B、512 C、128 D、64

    查看试题解析

二、填空题

  • 10. 分解因式： x2y−4y= ．

    查看试题解析

  • 11. 若一个多边形的内角和是 540° ，则该多边形的边数是.

    查看试题解析

  • 12. 比较大小：27508140（填“＞”“＜”或“＝”）．

    查看试题解析

  • 13. 若x2﹣2ax+16是完全平方式，则a= ．

    查看试题解析

  • 14. 有一三角形纸片ABC，∠A＝70°，点D是AC边上一点，沿BD方向剪开三角形纸片后，发现所得两个纸片均为等腰三角形，则∠C的度数可以是 ．

    查看试题解析

三、解答题

  • 15. 如图，△ABC中，∠B=40°，∠C=80°，AE是△ABC的高．

    (1)、画出△ABC的角平分线AD，并求出∠DAE的度数；
    (2)、直接写出∠B，∠C和∠DAE三者之间的数量关系．

    查看试题解析

  • 16. 计算：
    (1)、（x+1）2+x（x－2）－（x+1）（x－1）
    (2)、（x+y）2－x（2y－x）

    查看试题解析

  • 17. 如图，在平面直角坐标系中完成下列各题：（不写作法，保留作图痕迹）

    (1)、在图1中作出 △ABC 关于y轴对称的 △A1B1C1 ，并写出 A1 、 B1 、 C1 的坐标；
    (2)、在图2中x轴上画出点P，使PA+PB的值最小．

    查看试题解析

  • 18. 如图，边长为a、b的矩形，它的周长为14，面积为10，计算a2b+2ab+ab2的值．

    查看试题解析

  • 19. 如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且∠CAD=45°．

    (1)、求证：△ABD≌△CFD；
    (2)、已知BC=7，AD=5，求AF的长．

    查看试题解析

  • 20. （阅读材料）

    对于二次三项式a2+2ab+b2可以直接分解为（a+b）2的形式，但对于二次三项式a2+2ab－8b2 ， 就不能直接用公式了，我们可以在二次三项式a2+2ab－8b2中先加上一项b2 ， 使其成为完全平方式，再减去b2这项，（这里也可把－8b2拆成+b2与－9b2的和），使整个式子的值不变．

    于是有：

    a2+2ab－8b2

    =a2+2ab－8b2+b2－b2

    =（a2+2ab+b2）－8b2－b2

    =（a+b）2－9b2

    =[（a+b）+3b][（a+b）－3b]

    =（a+4b）（a－2b）

    我们把像这样将二次三项式分解因式的方法叫做添（拆）项法．

    （应用材料）

    (1)、上式中添（拆）项后先把完全平方式组合在一起，然后用法实现分解因式．
    (2)、请你根据材料中提供的因式分解的方法，将下面的多项式分解因式：

    ①m2+6m+8；

    ②a4+10a2b2+9b4

    查看试题解析

  • 21. 在学习完第12章后，张老师让同学们独立完成课本56页第9题：“如图1，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E，AD=2.5cm，DE=1.7cm，求BE的长．”

    (1)、请你也独立完成这道题；
    (2)、待同学们完成这道题后，张老师又出示了一道题：

    在课本原题其它条件不变的前提下，将CE所在直线旋转到△ABC的外部（如图2），请你猜想AD，DE，BE三者之间的数量关系，直接写出结论，不需证明．

    (3)、如图3，将（1）中的条件改为：在△ABC中，AC=BC，D，C，E三点在同一条直线上，并且有∠BEC=∠ADC=∠BCA=α，其中α为任意钝角，那么（2）中你的猜想是否还成立？若成立，请证明；若不成立，请说明理由．

    查看试题解析