江西省上饶市2020-2021学年九年级上学期数学第三次月考试卷
试卷更新日期:2021-01-21 类型:月考试卷
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 直线 不经过第二象限,则关于 的方程 实数解的个数是( ).A、0个 B、1个 C、2个 D、1个或2个3. 掷一枚质地均匀的硬币5次,其中3次正面朝上,2次正面朝下,则再次掷出这枚硬币,正面朝下的概率是( )A、1 B、 C、 D、4. 已知二次函数 ,则下列关于这个函数图象和性质的说法,正确的是( )A、图象的开口向上 B、图象的顶点坐标是 C、当 时,y随x的增大而增大 D、图象与x轴有唯一交点5. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( )
2. 直线 不经过第二象限,则关于 的方程 实数解的个数是( ).A、0个 B、1个 C、2个 D、1个或2个3. 掷一枚质地均匀的硬币5次,其中3次正面朝上,2次正面朝下,则再次掷出这枚硬币,正面朝下的概率是( )A、1 B、 C、 D、4. 已知二次函数 ,则下列关于这个函数图象和性质的说法,正确的是( )A、图象的开口向上 B、图象的顶点坐标是 C、当 时,y随x的增大而增大 D、图象与x轴有唯一交点5. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( ) A、57° B、52° C、38° D、26°6. 如图,已知 是 的两条切线,A , B为切点,线段 交 于点M . 给出下列四种说法:① ;② ;③四边形 有外接圆;④M是 外接圆的圆心,其中正确说法的个数是( )
A、57° B、52° C、38° D、26°6. 如图,已知 是 的两条切线,A , B为切点,线段 交 于点M . 给出下列四种说法:① ;② ;③四边形 有外接圆;④M是 外接圆的圆心,其中正确说法的个数是( )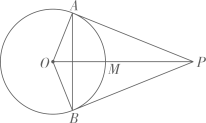 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
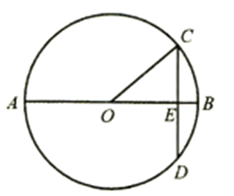
7. 如果关于x的一元二次方程 有两个相等的实数根,那么实数k的值是.8. 将抛物线y=(x-1)2-5关于y轴对称,再向右平移3个单位长度后顶点的坐标是 .9. 如图 是 的直径,弦 于点E,交 于点D,已知 , ,则 cm.
 10. 一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是.
10. 一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是.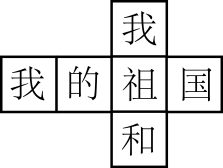 11. 如图,在 中, , .将 绕点A按顺时针方向旋转至 的位置,点 恰好落在边 的中点处,则 的长为 .
11. 如图,在 中, , .将 绕点A按顺时针方向旋转至 的位置,点 恰好落在边 的中点处,则 的长为 .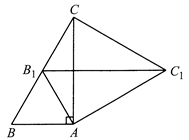 12. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .若抛物线 (h、k为常数)与线段 交于C、D两点,且 ,则k的值为 .
12. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .若抛物线 (h、k为常数)与线段 交于C、D两点,且 ,则k的值为 .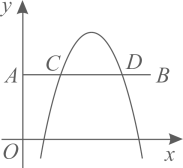
三、解答题
-
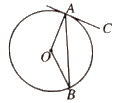
13.(1)、解方程:(2)、如图, 是 的弦, 与 相切于点 连接 ,若 求 的度数.
 14. 已知关于x的一元二次方程 有两个不相等的实数根.(1)、求k的取值范围;(2)、若方程的两个不相等的实数根是 ,求 的值.15. 如图①是山东舰徽的构图,采用航母 度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为 的圆锥侧面展开图(如图②),则该圆锥的母线长 为多少?
14. 已知关于x的一元二次方程 有两个不相等的实数根.(1)、求k的取值范围;(2)、若方程的两个不相等的实数根是 ,求 的值.15. 如图①是山东舰徽的构图,采用航母 度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为 的圆锥侧面展开图(如图②),则该圆锥的母线长 为多少? 16. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.
16. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.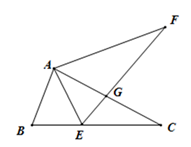 (1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.17. 某校计划组建航模、摄影、乐器、舞蹈四个课外活动小组,要求每名同学必须参加,并且只能选择其中一个小组.为了解学生对四个课外活动小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把此次调查结果整理并绘制成如图两幅不完整的统计图.
(1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.17. 某校计划组建航模、摄影、乐器、舞蹈四个课外活动小组,要求每名同学必须参加,并且只能选择其中一个小组.为了解学生对四个课外活动小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把此次调查结果整理并绘制成如图两幅不完整的统计图.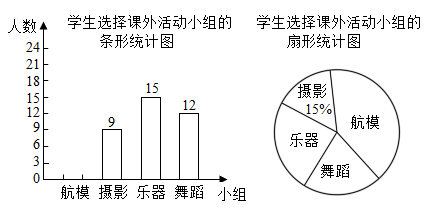
根据图中提供的信息,解答下列问题:
(1)、本次被调查的学生有人;(2)、请补全条形统计图,并求出扇形统计图中“航模”所对应的圆心角的度数.18. 如图,在平面直角坐标系中, 的三个顶点分别是 .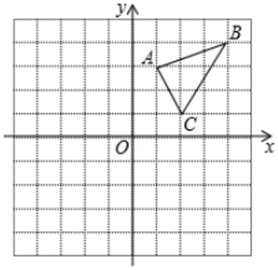
把 向左平移 个单位后得到对应的 ,请画出平移后的 ;
把 绕原点O旋转 后得到对应的 ,请画出旋转后的 .
19. 某校组织开展运动会,小明和扎西两名同学准备从100米短跑(记为项目A),800米中长跑(记为项目B),跳远(记为项目C),跳高(记为项目D),即从A,B,C,D四个项目中,分别选择一个项目参加比赛.请用画树状图或列表法求两名同学选到相同项目的概率.20. 如图所示, 是 的直径, 和 分别切 于 两点, 与 有公共点 且 .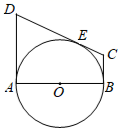 (1)、求证: 是 的切线;(2)、若 ,求 的长,21. 某服装厂生产 品种服装,每件成本为71元,零售商到此服装厂一次性批发 品牌服装 件时,批发单价为 元, 与 之间满足如图所示的函数关系,其中批发件数 为10的正整数倍.
(1)、求证: 是 的切线;(2)、若 ,求 的长,21. 某服装厂生产 品种服装,每件成本为71元,零售商到此服装厂一次性批发 品牌服装 件时,批发单价为 元, 与 之间满足如图所示的函数关系,其中批发件数 为10的正整数倍.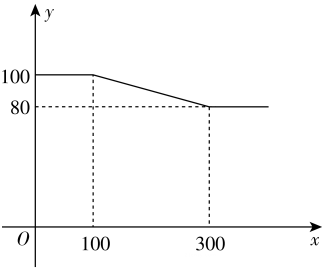 (1)、当 时, 与 的函数关系式为.(2)、某零售商到此服装厂一次性批发 品牌服装200件,需要支付多少元?(3)、零售商到此服装厂一次性批发 品牌服装 件,服装厂的利润为 元,问: 为何值时, 最大?最大值是多少?22. 如图1,点B在线段 上,Rt△ ≌Rt△ , , , .
(1)、当 时, 与 的函数关系式为.(2)、某零售商到此服装厂一次性批发 品牌服装200件,需要支付多少元?(3)、零售商到此服装厂一次性批发 品牌服装 件,服装厂的利润为 元,问: 为何值时, 最大?最大值是多少?22. 如图1,点B在线段 上,Rt△ ≌Rt△ , , , .
 (1)、点F到直线 的距离是;(2)、固定△ ,将△ 绕点C按顺时针方向旋转30°,使得 与 重合,并停止旋转.
(1)、点F到直线 的距离是;(2)、固定△ ,将△ 绕点C按顺时针方向旋转30°,使得 与 重合,并停止旋转.①请你在图1中用直尺和圆规画出线段 经旋转运动所形成的平面图形(用阴影表示,保留画图痕迹,不要求写画法)该图形的面积为;
②如图2,在旋转过程中,线段 与 交于点O,当 时,求 的长.
23. 如图,二次函数 的图象交x轴于点 , ,交y轴于点C.点 是x轴上的一动点, 轴,交直线 于点M,交抛物线于点N. (1)、求这个二次函数的表达式;(2)、①若点P仅在线段 上运动,如图1.求线段 的最大值;
(1)、求这个二次函数的表达式;(2)、①若点P仅在线段 上运动,如图1.求线段 的最大值;②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.