江西省赣州市2020-2021学年九年级上学期数学第二次月考试卷
试卷更新日期:2021-01-21 类型:月考试卷
一、单选题
-
1. 下列事件中,是随机事件的是( )A、明天太阳从西边出来 B、打开电视,正在播放《江西新闻》 C、南昌是江西的省会 D、小明跑完1000米所用的时间恰好为1分钟2. 江西景德镇的青花瓷是中华陶瓷工艺的珍品,下列青花瓷上的青花图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知半径为10的⊙O和直线l上一点A,且 ,则直线l与⊙O的位置关系是( )A、相切 B、相交 C、相交或相离 D、相切或相交4. 如图,AB是⊙O的直径,C、D为⊙O上的点,弧AD=弧CD , 若∠CAB=40°,则∠CAD=( )
3. 已知半径为10的⊙O和直线l上一点A,且 ,则直线l与⊙O的位置关系是( )A、相切 B、相交 C、相交或相离 D、相切或相交4. 如图,AB是⊙O的直径,C、D为⊙O上的点,弧AD=弧CD , 若∠CAB=40°,则∠CAD=( )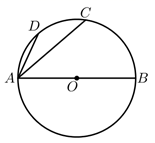 A、30° B、40° C、50° D、25°5. 当 时,关于 的一元二次方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 对于抛物线y=ax2+4ax﹣m(a≠0)与x轴的交点为A(﹣1,0),B(x2 , 0),则下列说法:
A、30° B、40° C、50° D、25°5. 当 时,关于 的一元二次方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 对于抛物线y=ax2+4ax﹣m(a≠0)与x轴的交点为A(﹣1,0),B(x2 , 0),则下列说法:①一元二次方程ax2+4ax﹣m=0的两根为x1=﹣1,x2=﹣3;
②原抛物线与y轴交于点C , CD∥x轴交抛物线于D点,则CD=4;
③点E(1,y1)、点F(﹣4,y2)在原抛物线上,则y1>y2;
④抛物线y=﹣ax2﹣4ax+m与原抛物线关于x轴对称.其中正确的有( )
A、4个 B、3个 C、2个 D、1个二、填空题
-
7. 把抛物线 向上平移2个单位,所得抛物线是 .8. 已知a、b是一元二次方程x2-2x-2020=0的两个根,则2a+2b-ab的值为 .9. 《九章算术》是我国古代内容极为丰富的数学名著.书中有下面问题“今有勾八步,股十五步,问勾中容圆径几何.”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”.请你计算其结果为步.10. 如图,在正六边形ABCDEF中,分别以C , F为圆心,以边长为半径作弧,图中阴影部分的面积为24π,则正六边形的边长为 .
 11. 加工爆米花时,爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下,可食用率 与加工时间 (单位: )满足函数表达式 ,则最佳加工时间为 .12. 中, , ,点O是AB的中点,将OB绕点O向三角形外部旋转 角时( ),得到OP , 当 恰为等腰三角形时, 的值为 .
11. 加工爆米花时,爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下,可食用率 与加工时间 (单位: )满足函数表达式 ,则最佳加工时间为 .12. 中, , ,点O是AB的中点,将OB绕点O向三角形外部旋转 角时( ),得到OP , 当 恰为等腰三角形时, 的值为 .三、解答题
-
13.(1)、解方程: ;(2)、如图所示,在 纸片中, ,将 纸片绕点A按逆时针方向旋转 ,得到 ,此时AD边经过点C , 连接BD , 若 的度数为 ,求 的度数.
 14. 已知关于x的二次函数 的图象经过点 , .(1)、求b、c的值;(2)、求出此二次函数的图象的顶点坐标及其与y轴的交点坐标.15. 如图,△ABC是⊙O的内接三角形,∠ABC=45°,请用无刻度的直尺按要求作图.
14. 已知关于x的二次函数 的图象经过点 , .(1)、求b、c的值;(2)、求出此二次函数的图象的顶点坐标及其与y轴的交点坐标.15. 如图,△ABC是⊙O的内接三角形,∠ABC=45°,请用无刻度的直尺按要求作图.
⑴如图1,请在图1中画出弦CD,使得CD=AC.
⑵如图2,AB是⊙O的直径,AN是⊙O的切线,点B,C,N在同一条直线上请在图中画出△ABN的边AN上的中线BD.
16. 随着信息技术的迅猛发展,移动支付如今已成为一种世界性的时代趋势.在一次购物中,刘老师和王老师都想从“微信”“支付宝”“银行卡”三种支付方式中选一种方式进行支付.(1)、王老师选择“微信”支付的概率是;(2)、请用列表法或画树状图法,求两位老师恰好一人选择“微信”支付,一人选择“银行卡”支付的概率.17. 如图,∠C=90°,以AC为半径的圆C与AB相交于点D.若AC=3,CB=4,求BD长.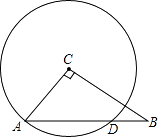 18. 如图所示的正方形网格中(每个小正方形的边长是1,小正方形的顶点叫作格点),△ABC的顶点均在格点上,请在所给平面直角坐标系中按要求画图和解答下列问题:
18. 如图所示的正方形网格中(每个小正方形的边长是1,小正方形的顶点叫作格点),△ABC的顶点均在格点上,请在所给平面直角坐标系中按要求画图和解答下列问题: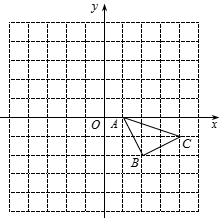 (1)、①以点C为旋转中心,将△ABC绕点C顺时针旋转90°得△CA1B1 , 画出△CA1B1;
(1)、①以点C为旋转中心,将△ABC绕点C顺时针旋转90°得△CA1B1 , 画出△CA1B1;②作出△ABC关于点A成中心对称的△AB2C2;
(2)、设AC2与y轴交于点D , 则△B1DC的面积为 .19. 关于x的一元二次方程 有两个实数根 , .(1)、求k的取值范围;(2)、是否存在实数k , 使得 和 互为相反数?若存在,请求出k的值;若不存在,请说明理由.20. 某地摊上的一种玩具,已知其进价为50元个,试销阶段发现将售价定为80元/个时,每天可销售20个,后来为了扩大销售量,适当降低了售价,销售量y(个)与降价x(元)的关系如图所示.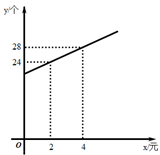
(1)、
求销量y与降价x之间的关系式;(2)、该玩具每个降价多少元,可以恰好获得750元的利润?(3)、若要使得平均每天销售这种玩具的利润W最大,则每个玩具应该降价多少元?最大的利润W为多少元?21. 如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.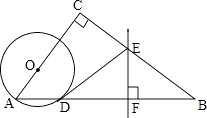 (1)、判断直线DE与⊙O的位置关系,并说明理由;(2)、若AC=6,BC=8,OA=2,求线段DE的长.22. 已知抛物线 中(a , b是常数)与y轴的交点为A , 点A与点B关于抛物线的对称轴对称,二次函数 中(b , c是常数)的自变量x与函数值y的部分对应值如下表:,
(1)、判断直线DE与⊙O的位置关系,并说明理由;(2)、若AC=6,BC=8,OA=2,求线段DE的长.22. 已知抛物线 中(a , b是常数)与y轴的交点为A , 点A与点B关于抛物线的对称轴对称,二次函数 中(b , c是常数)的自变量x与函数值y的部分对应值如下表:,…
0
1
3
4
…
…
8
0
0
…
(1)、下列结论正确的是A . 抛物线的对称轴是
B . 当 时,y有最大值
C . 当 时,随x的增大而增大
D . 点A的坐标是 ,点B的坐标是
(2)、求二次函数 的解析式(3)、已知点 在抛物线 上,设 的面积为S , 求S与m的函数关系式画出函数图象.并利用函数图象说明S是否存在最大值,为什么?23. 问题背景:如图1,在 中, , , ,四边形 是正方形,求图中阴影部分的面积.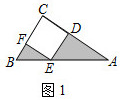 (1)、发现:如图2,小芳发现,只要将 绕点 逆时针旋转一定的角度到达 ,就能将阴影部分转化到一个三角形里,从而轻松解答.根据小芳的发现,可求出图1中阴影部分的面积为;(直接写出答案)
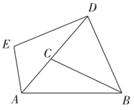
(1)、发现:如图2,小芳发现,只要将 绕点 逆时针旋转一定的角度到达 ,就能将阴影部分转化到一个三角形里,从而轻松解答.根据小芳的发现,可求出图1中阴影部分的面积为;(直接写出答案)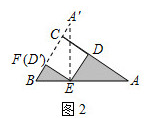 (2)、应用:如图3,在四边形 中, , , 于点 ,若四边形 的面积为16,试求出 的长;
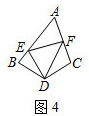
(2)、应用:如图3,在四边形 中, , , 于点 ,若四边形 的面积为16,试求出 的长;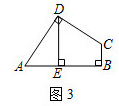 (3)、拓展:如图4,在四边形 中, , , ,以 为顶点作 为 角,角的两边分别交 , 于 , 两点,连接 ,请直接写出线段 , , 之间的数量关系.
(3)、拓展:如图4,在四边形 中, , , ,以 为顶点作 为 角,角的两边分别交 , 于 , 两点,连接 ,请直接写出线段 , , 之间的数量关系.