福建省南平市顺昌县2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-01-21 类型:月考试卷
一、单选题
-
1. 方程 的根是( )A、 B、 C、 D、以上答案都不对2. 抛物线y=x2﹣2x+1与y轴的交点坐标为( )A、(1,0) B、(0,1) C、(0,0) D、(0,2)3. 一元二次方程x2+5x+3=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定4. 将抛物线 向右平移1个单位,再向上平移5个单位后所得抛物线的解析式为( )A、 B、 C、 D、5. 已知等腰三角形的腰和底的长分别是一元二次方程x2﹣4x+3=0的根,则该三角形的周长可以是( )A、5 B、7 C、5或7 D、106. 已知A(﹣3,y1)、B(﹣2,y2)、C(2,y3)在二次函数y=x2+2x+c的图象上,比较y1、y2、y3的大小( )A、y1>y2>y3 B、y2>y3>y1 C、y2>y1>y3 D、y3>y1>y27. 一元二次方程 配方后化为( )A、 B、 C、 D、8. 某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队数是( )A、6 B、7 C、8 D、99. 如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b-1)x+c的图象可能是( )
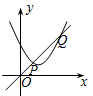 A、
A、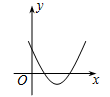 B、
B、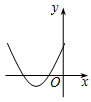 C、
C、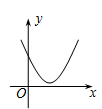 D、
D、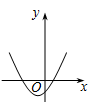 10. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,与x轴的一个交点坐标为(4,0),抛物线的对称轴是x=1.下列结论中:①abc<0;②2a+b=0;③3a+c>0;④关于x的方程ax2+bx+c-2=0有两个不相等的非零实数根m、n(m<n)则-2< m<n<4;⑤若点A(m,n)在该抛物线上,则am2+bm≤a+b;其中正确的有( )
10. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,与x轴的一个交点坐标为(4,0),抛物线的对称轴是x=1.下列结论中:①abc<0;②2a+b=0;③3a+c>0;④关于x的方程ax2+bx+c-2=0有两个不相等的非零实数根m、n(m<n)则-2< m<n<4;⑤若点A(m,n)在该抛物线上,则am2+bm≤a+b;其中正确的有( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
11. 抛物线 的顶点坐标是.12. 若关于x的方程x2+ax+a=0有一个根为﹣3,则a的值是.13. 用一根长为80cm的铁丝,把它弯成一个矩形,设矩形的面积为ycm2 , 一边长为xcm,则y与x的函数表达式为(化为一般式)14. 若关于x的方程(a+3)x|a|-1﹣3x+2=0是一元二次方程,则a的值为 .15. 向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0),若此炮弹在第6秒与第16秒时的高度相等,则炮弹所在高度最高的是第秒.16. 设函数y=x2+2kx+k-1(k为常数),下列说法中:(1)对任意实数k,函数与x轴有两个交点;(2)当x≥-k时,函数y的值都随x的增大而减小;(3)k取不同的值时,二次函数y的顶点始终在同一条抛物线上;(4)对任意实数k,抛物线y=x2+2kx+k-1都必定经过唯一定点.正确的说法有(填写序号) .
三、解答题
-
17. 解下列方程:(1)、2(2x-1)2=8;(2)、x2-3x-2 =0.18. 已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(0,1),B(2,1)和C(3,4).
 (1)、求该二次函数的解析式;(2)、在平面直角坐标系中画出该函数的大致图象,并写出图象的对称轴.19. 关于x的一元二次方程 ,求证:方程总有两个实数根.20. 为建设美丽家园,某企业逐年增加对环境保护的经费投入,2015年投入了400万元,到2017年投入了576万元.
(1)、求该二次函数的解析式;(2)、在平面直角坐标系中画出该函数的大致图象,并写出图象的对称轴.19. 关于x的一元二次方程 ,求证:方程总有两个实数根.20. 为建设美丽家园,某企业逐年增加对环境保护的经费投入,2015年投入了400万元,到2017年投入了576万元.
(1)、求2015年至2017年该单位环保经费投入的年平均增长率;
(2)、该单位预计投入环保经费不低于700万元,若希望继续保持前两年的年平均增长率,问该目标能否实现?请通过计算说明理由.
21. 杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y= x2+3x+1的一部分,如图所示. (1)、求演员弹跳离地面的最大高度;
(1)、求演员弹跳离地面的最大高度;
(2)、已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
22. 如图:在△ABC中,∠ABC=90°,AB=BC=8cm,动点P从点A出发,以2cm/s的速度沿射线AB运动,同时动点Q从点C出发,以2cm/s的速度沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t秒,△PCQ的面积为S cm2 . (1)、直接写出AC的长:AC=cm;(2)、求出S关于t的函数关系式,并求出当点P运动几秒时,S△PCQ=S△ABC23. 阅读材料:
(1)、直接写出AC的长:AC=cm;(2)、求出S关于t的函数关系式,并求出当点P运动几秒时,S△PCQ=S△ABC23. 阅读材料:材料1:若一元二次方程ax2+bx+c=0(a≠0)的两根为x1、x2 , 则x1+x2= ,x1x2= .
材料2:已知实数m、n满足m2-m-1=0,n2-n-1=0,且m≠n,求 的值.
解:由题知m、n是方程x2-x-1=0的两个不相等的实数根,根据材料1,得m+n=1,mn=-1.
∴ .
根据上述材料解决下面的问题:
(1)、一元二次方程x2-4x-3=0的两根为x1、x2 , 则x1+x2=4,x1x2=;(2)、已知实数m,n满足 , ,且m≠n,求m2n+mn2的值;
(3)、已知实数p,q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2的值.24. 某公司销售一种商品,成本为每件30元,经过市场调查发现,该商品的日销售量y(件)与销售单价x(元)是一次函数关系,其销售单价、日销售量的三组对应数值如下表:销售单价x(元)
40
60
80
日销售量y(件)
80
60
40
(1)、直接写出y与x的关系式;(2)、求公司销售该商品获得的最大日利润;(3)、销售一段时间以后,由于某种原因,该商品每件成本增加了10元,若物价部门规定该商品销售单价不能超过a元,在日销售量y(件)与销售单价x(元)保持(1)中函数关系不变的情况下,该商品的日销售最大利润是1500元,求a的值.25. 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象与直线AB交于A、B两点,A(1,﹣ )、B(﹣2,0),其中点A是抛物线y=ax2+bx+c的顶点,交y轴于点D.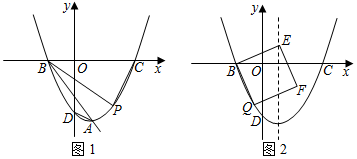 (1)、求二次函数解析式;(2)、如图1,点P是第四象限抛物线上一动点,若∠PBA=∠BAD,抛物线交x轴于点C.求△BPC的面积;(3)、如图2,点Q是第三象限内抛物线上一点(不与点B、D重合),连接BQ,以BQ为边作正方形BEFQ,当顶点E或F恰好落在抛物线对称轴上时,直接写出对应的Q点的坐标.
(1)、求二次函数解析式;(2)、如图1,点P是第四象限抛物线上一动点,若∠PBA=∠BAD,抛物线交x轴于点C.求△BPC的面积;(3)、如图2,点Q是第三象限内抛物线上一点(不与点B、D重合),连接BQ,以BQ为边作正方形BEFQ,当顶点E或F恰好落在抛物线对称轴上时,直接写出对应的Q点的坐标.