广东省深圳市深实验2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-01-21 类型：期末考试

进入出卷网下载

一、选择题(每小题3分，共30分)

1. 实数2020的相反数是（）

A、2020 B、 $\frac{1}{2020}$ C、-2020 D、 $- \frac{1}{2020}$

查看试题解析
2. 下列图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 太阳中心的温度高达19 200000℃，用科学记数法将19 200 000℃可表示为（）

A、1.92×10⁶ B、1.92×10⁷ C、19.2×10⁶ D、19.2×10⁷

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、a+2a=2a² C、x（1+y）=x+xy D、（mn²）³=mn⁶

查看试题解析
5. 如图，转盘中四个扇形的面积都相等，小明随意转动转盘1次，指针指向的数字为偶数的概率为（）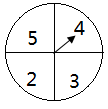

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、 $\frac{5}{6}$

查看试题解析
6. 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：
成绩/m
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
则这些运动员成绩的中位数、众数分别为（）

A、1.70，1.75 B、1.70，1.70 C、1.65，1.75 D、1.65，1.70

查看试题解析
7. 某文具店一本练习本和一支水笔的单价合计为3元，小妮在该店买了20本练习本和10支水笔，共花了36元．如果设练习本每本为x元，水笔每支为y元，那么根据题意，下列方程组中，正确的是（）

A、 ${\begin{cases} x - y = 3 \\ 20 x + 10 y = 36 \end{cases}$ B、 ${\begin{cases} x + y = 3 \\ 20 x + 10 y = 36 \end{cases}$ C、 ${\begin{cases} y - x = 3 \\ 20 x + 10 y = 36 \end{cases}$ D、 ${\begin{cases} y + x = 3 \\ 10 x + 20 y = 36 \end{cases}$

查看试题解析
8. 如图，在△ABC，B．A=BC，∠B=80°，观察图中尺规作图的痕迹，则∠DCE的度数为（）

A、60° B、65° C、70° D、75°

查看试题解析
9. 已知二次函数y=ax²+bx+c的图象如图所示，对称轴为直线x=1，则下列结论正确的是（）

A、ac>0 B、当x>0，y随x的增大而减小 C、2a-b=0 D、方程ax²+bx+c=0的两根是x₁=-1，x₂=3

查看试题解析
10. 如图，正方形ABCD和正方形CGFE的顶点C，D，E在同一直线上，顶点B，C，G在同一条直线上，O是EG的中点，∠EGC的平分线GH过点D，交BE于点H，连接FH交EG于点M，连接OH。以下四个结论：①GH⊥BE；②△EHM∽△FHG；③ $\frac{B C}{C G} = \sqrt{2} - 1$ ； $\frac{S_{△ H O M}}{S_{△ H O G}} = 2 - \sqrt{2}$ ，其中正确的结论是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题(每小题3分，共15分)

11. 分解因式：ab²-a= 。

查看试题解析
12. 已知x=2是一元二次方程x²-mx+2=0的一个解，则m的值是。

查看试题解析
13. 如图，已知AB是⊙O的直径，AB=2，C、D是圆周上的点，且sin∠CDB= $\frac{1}{3}$ ，则BC的长为。

查看试题解析
14. 如图，在矩形ABCD中，对角线4C与BD相交于点O，CE⊥BD，垂足为点E，CE=5，且OE=2DE，则DE的长为。

查看试题解析
15. 如图，点A4(1，3)为双曲线y= $\frac{3}{x}$ 上的一点，连接40并延长与双曲线在第三象限交于点B，M为y轴正半轴上一点，连接MA并延长与双曲线交于点N，连接BM、BN，已知△MBN的面积为 $\frac{33}{2}$ ，则点N的坐标为。

查看试题解析

三、解答题(第16题5分，第17题6分，第18--20 题每题8分，第21- -22题每题10分，共55分)

16. 计算： |2- $\sqrt{3}$ |+2sin60°+( $\frac{1}{2}$ )^-1-( $\sqrt{2015}$ )⁰

查看试题解析
17. 先化简，再求值： $(\frac{3 x}{x - 2} - \frac{x}{x + 2}) \div \frac{x}{x^{2} - 4}$ ，在-2，0，1，2四个数中选一个合适的代入求值。

查看试题解析
18. 为了解某校九年级男生1000米跑的水平，从中随机抽取部分男生进行测试，并把测试成绩分为A、B、C、D四个等次，绘制成如图所示的不完整的统计图，请你依图解答下列问题：

(1)、a= ， b= ， c= 。

(2)、将条形统计图补充完整，并计算表示C等次的扇形所对的圆心角的度数为°。

(3)、学校决定从4等次的甲、乙、丙、丁四名男生中，随机选取两名男生参加全市中学生1000米跑比赛，请用列表法或画树状图法，求甲、乙两名男生同时被选中的概率。

查看试题解析
19. 如图， $B C$ 是 $⊙ O$ 的直径， $C E$ 是 $⊙ O$ 的弦，过点 $E$ 作 $⊙ O$ 的切线，交 $C B$ 的延长线于点 $G$ ，过点 $B$ 作 $B F ⊥ G E$ 于点 $F$ ，交 $C E$ 的延长线于点 $A$ ．

(1)、求证： $∠ A B G = 2 ∠ C$ ；

(2)、若 $G F = 3 \sqrt{3}$ ， $G B = 6$ ，求 $⊙ O$ 的半径．

查看试题解析
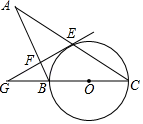20. 某小区为了绿化环境，计划分两次购进A、B两种数苗30棵，第一次购进4种树苗30棵，B种树苗15棵，共花费1 350元；第二次购进4种树苗24棵，B种树苗10棵，共花费1060元。(两次购进A，B两种树苗各自的单价均不变)

(1)、A，B两种树苗每棵的价格分别是多少元？

(2)、若购买A，B两种树苗共42棵，总费用为W元，购买4种树苗t棵，B种树苗的数量不超过4种树苗数量的2倍，求W与t的函数关系式．请设计出最省钱的购买方案，并求出此方案的总费用。

查看试题解析
21. 已知等边△ABC的边长为8，点P是AB边上的一个动点(与点A、B不重合)。

(1)、如图1，当PB=3PA时，△BPC的面积为；

(2)、直线1是经过点P的一条直线，把△ABC沿直线1折叠，点B的对应点是点B'．
①如图2，当PB=5时，若直线l∥AC，求BB'的长度；

②如图3，当PB=6时，在直线l变化过程中，请直接写出△ACB'面积的最大值。

查看试题解析
22. 在平面直角坐标系xOy中，已知抛物线y=ax²+bx+c与x轴交于A(-1，0)，B(4，0)两点，与y轴交于点C(0，-2)。

(1)、求抛物线的函数解析式；

(2)、如图1，点D为第四象限抛物线上一点，连接AD，BC交于E，求 $\frac{D E}{A E}$ 的最大值；

(3)、如图3，连接AC，BC，过点0作直线l∥BC，点P，Q分别为直线1和抛物线上的点。试探究：在第一象限是否存在这样的点P，Q，使△PQB∽△CAB。若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由。

查看试题解析

成绩/m	1.50	1.60	1.65	1.70	1.75	1.80
人数	2	3	2	3	4	1