浙江省宁波市江北区2020-2021学年七年级上学期数学第三次月考试卷

试卷更新日期：2021-01-20 类型：月考试卷

进入出卷网下载

一、单选题（共10题；共30分）

1. ﹣3的相反数是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、-3 D、3

查看试题解析
2. 2019年6月21日甬台温高速温岭联络线工程初步设计通过，本项目为沿海高速和甬台温高速公路之间的主要联络通道，总投资1289000000元，这个数据用科学记数法表示为（）

A、0.1289×10¹¹ B、1.289×10¹⁰ C、1.289×10⁹ D、1289×10⁷

查看试题解析
3. 下列数或式：（-2）³ ， ${(- \frac{1}{3})}^{6}$ ，-5²,0，m²+1数轴上所对应的点一定在原点右边的个数是（）

A、 1 B、2 C、3 D、4

查看试题解析
4. $\sqrt{81}$ 的平方根是（）

A、9 B、9或－9 C、3 D、3或－3

查看试题解析
5. 根据等式的性质，下列变形正确的是（）

A、若2a＝3b，则a＝ $\frac{2}{3}$ b B、若a＝b，则a+1＝b﹣1 C、若a＝b，则2﹣ $\frac{a}{3}$ ＝2﹣ $\frac{b}{3}$ D、若 $\frac{a}{2} = \frac{b}{3}$ ，则2a＝3b

查看试题解析
6. 解方程 $\frac{1.5 x}{0.6} - \frac{1.5 - x}{2} = 0.5$ ，以下变形正确的是（）

A、 $\frac{5 x}{2} - \frac{15 - x}{2} = 5$ B、 $\frac{5 x}{2} - \frac{15 - 10 x}{2} = 5$ C、 $\frac{5 x}{2} - \frac{15 - x}{20} = 0.5$ D、 $\frac{5 x}{2} - \frac{3 - 2 x}{4} = 0.5$

查看试题解析
7. 已知单项式﹣3a^m^﹣¹b⁶与 $\frac{1}{5}$ ab²ⁿ是同类项，则m+n的值是（）

A、 0 B、3 C、4 D、5

查看试题解析
8. 如图，小明用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能解释这一现象的数学知识是（）

A、经过一点能画无数条直线 B、两点之间，线段最短 C、两点确定一条直线 D、连接两点间的线段的长度，叫做这两点的距离

查看试题解析
9. 三江夜游项目是宁波市月光经济和“三江六岸”景观提升的重要工程，一艘游轮从周宿夜江游船码头到宁波大剧院游船码头顺流而行用40分钟，从宁波大剧院游船码头沿原线返回周宿夜江游船码头用了1小时，已知游轮在静水中的平均速度为8千米/小时，求水流的速度。设水流的速度为x千米/小时，则可列方程为（）

A、40(8-x)=1×(8+x) B、 $\frac{2}{3}$ (8+x)=8 C、 $\frac{2}{3}$ (8+x)=8-x D、 $\frac{8 + x}{40} = \frac{8 - x}{60}$

查看试题解析
10. 已知线段AB=a，C，D，E分别是AB，BC，AD的中点，分别以点C，D，E为圆心，CB，DB，EA为半径作圆得如图所示的图案，则图中三个阴影部分图形的周长之和为（）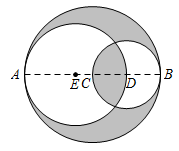

A、9πa B、8πa C、 $\frac{9}{8}$ πa D、 $\frac{9}{4}$ πa

查看试题解析

二、填空题（共6题；共24分）

11. |-3| =

查看试题解析
12. 多项式3x²y-2x²y²-5 次项式.

查看试题解析
13. 已知x=3是方程ax=a+10的解，则a的值是。

查看试题解析
14. $\sqrt{9}$ 算术平方根是

查看试题解析
15. 请写出一个解为x=-1一元一次方程：

查看试题解析
16. “格子乘法”作为两个数相乘的一种计算方法最早在15世纪由意大利数学家帕乔利提出，在明代的《算法统宗》一书中被称为“铺地锦”。如图1，计算47x51，将乘数47计入上行，乘数51计入右行，然后以乘数47的每位数字乘以乘数51的每位数字，将结果计入相应的格子中，最后按斜行加起来，得2397。

（ 1 ）如图2，用“格子乘法”表示25×81，则m的值为。

（ 2 ）如图3，用“格子乘法”表示两个两位数相乘，则a的值为。

查看试题解析

三、解答题（共7题；共66分）

17. 计算：

(1)、(-1)²+ ${}^{3}{\sqrt{- 27}}$ +|-2|

(2)、 ${(- 6)}^{2} \times (\frac{1}{3} - \frac{1}{2}) - 2^{3}$

查看试题解析
18. 解方程：

(1)、8-x=3x+2

(2)、 $\frac{x}{5} - \frac{3 - 2 x}{2} = x$

查看试题解析
19. 对于有理数a，b，定义一种新运算“⊗”，规定a⊗b＝|a+b|﹣|a﹣b|.

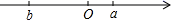(1)、计算（﹣3）⊗2的值；

(2)、当a，b在数轴上的位置如图所示时，化简a⊗b.

查看试题解析
20. 先化简，再求值： $\frac{1}{2}$ (8x²-3xy)-3(x²- $\frac{1}{2}$ xy+ $\frac{1}{3}$ y)，其中x=-2，y=1。

查看试题解析
21. 列方程解应用题：
冬季来临，某电器商城试销A，B两种型号的电暖器，两周内共销售50，销售收入14400，A型号电暖器每台300，B型号电暖器每台280.试销期间A，B两种型号的电暖器各销售了多少台？

查看试题解析
22. 观察下面的三行单项式
x，2x² ， 4x³ ， 8x⁴ ， 16x⁵…①

﹣2x，4x² ， ﹣8x³ ， 16x⁴ ， ﹣32x⁵…②

2x，﹣3x² ， 5x³ ， ﹣9x⁴ ， 17x⁵…③

根据你发现的规律，完成以下各题：

(1)、第①行第8个单项式为；第②行第2020个单项式为.

(2)、第③行第n个单项式为.

(3)、取每行的第9个单项式，令这三个单项式的和为A.计算当x＝ $\frac{1}{2}$ 时，256（A+ $\frac{1}{4}$ ）的值.

查看试题解析
23. 在数轴上点A表示整数a，且 $\sqrt{55} < a < \sqrt{65}$ ，点B表示a的相反数.

(1)、画数轴，并在数轴上标出点A与点B；

(2)、点P， Q 在线段AB上，且点P在点Q的左侧，若P， Q两点沿数轴相向匀速运动，出发后经4秒两点相遇. 已知在相遇时点Q比点P多行驶了3个单位，相遇后经1秒点Q到达点P的起始位置. 问点P、Q运动的速度分别是每秒多少个单位；.

(3)、在(2)的条件下，若点P从整数点出发，当运动时间为t秒时(t是整数)，将数轴折叠，使A点与B点重合，经过折叠P点与Q点也恰好重合，求P点的起始位置表示的数.

查看试题解析