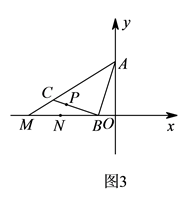浙江省宁波市江北区2020-2021学年八年级上学期数学第三次月考试卷
试卷更新日期:2021-01-20 类型:月考试卷
一、单选题(每小题3分,共36分)
-
1. 下列图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组数中,不可能成为一个三角形三边长的是( )A、5,6,12 B、2,3,4 C、5,7,7 D、6,8,103. 下列是一元一次不等式的有
2. 下列各组数中,不可能成为一个三角形三边长的是( )A、5,6,12 B、2,3,4 C、5,7,7 D、6,8,103. 下列是一元一次不等式的有, , , , , , .
A、1个 B、2个 C、3个 D、4个4. 平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )A、y轴对称 B、x轴对称 C、原点对称 D、直线y=x对称5. 若点( , )在函数 的图象上,则 的值是( )A、2 B、-2 C、8 D、-16. 已知等腰三角形的两边长分别为3和6,则它的周长等于( )
A、12 B、12或15 C、15 D、15或187. 下列命题中的真命题是( )A、锐角大于它的余角 B、锐角大于它的补角 C、钝角大于它的补角 D、锐角与钝角之和等于平角8. 若不等式组 无正整数解,则a的取值范围为( )A、a≤15 B、a<9 C、a<15 D、a≤99. 已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标是( )A、(﹣4,0) B、(6,0) C、(﹣4,0)或(6,0) D、(0,12)或(0,﹣8)10. 关于函数y=(k﹣3)x+k,给出下列结论:①此函数是一次函数,②无论k取什么值,函数图象必经过点(﹣1,3),③若图象经过二、三、四象限,则k的取值范围是k<0,④若函数图象与x轴的交点始终在正半轴可得k<3.其中正确的是( )
A、①② B、①③ C、②③ D、③④11. 如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=108°,则∠C的度数为( )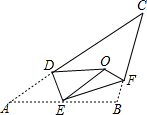 A、40° B、41° C、32° D、36°12. 如图,在△ABC中,∠C=90°,AC=BC= ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).
A、40° B、41° C、32° D、36°12. 如图,在△ABC中,∠C=90°,AC=BC= ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).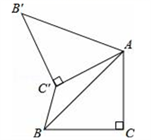 A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题(每小题4分,共24分)
-
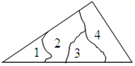
13. 写出一个与 的图象平行的函数.14. 已知平面直角坐标系内点P的坐标为(-1,3),如果将平面直角坐标系向左平移3个单位,再向下平移2个单位,那么平移后点P的坐标为15. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第块。
 16. 对于正整数a、b、c、d,符号 表示运算ac-bd,已知1< <3,则b+d=.17. 在△ABC中,AB=AC=5,BC=6,若点P在边AB上移动,则CP的最小值是.
16. 对于正整数a、b、c、d,符号 表示运算ac-bd,已知1< <3,则b+d=.17. 在△ABC中,AB=AC=5,BC=6,若点P在边AB上移动,则CP的最小值是.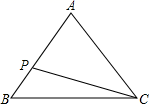 18. 如图,在平面直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A,B,C按逆时针排列),当点B运动到原点O处时,则点C的坐标是.随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的表达式是.
18. 如图,在平面直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A,B,C按逆时针排列),当点B运动到原点O处时,则点C的坐标是.随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的表达式是.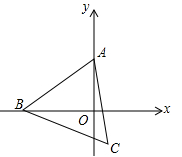
三、解答题(第19、20题每小题8分,第21、22题每小题10分,第23、24题每小题12分,共60分)
-
19. 解不等式组 ,并求出它的所有整数解的和.20. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).
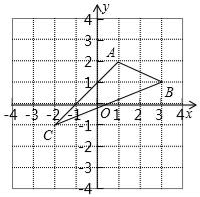 (1)、在图中作出△ABC关于 轴对称的△A1B1C1;(2)、写出点A1 , B1 , C1的坐标(直接写答案):A1 , B1 , C1.21. 如图,“开心”农场准备用 的护栏围成一块靠墙的矩形花园,设矩形花园的长为 ,宽为 .
(1)、在图中作出△ABC关于 轴对称的△A1B1C1;(2)、写出点A1 , B1 , C1的坐标(直接写答案):A1 , B1 , C1.21. 如图,“开心”农场准备用 的护栏围成一块靠墙的矩形花园,设矩形花园的长为 ,宽为 .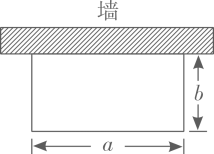 (1)、当 时,求b的值;(2)、受场地条件的限制,a的取值范围为 ,求b的取值范围.22. 如图:在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE, 垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)、当 时,求b的值;(2)、受场地条件的限制,a的取值范围为 ,求b的取值范围.22. 如图:在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE, 垂足为F,过B作BD⊥BC交CF的延长线于D.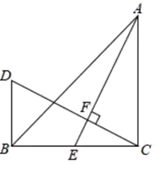
求证:
(1)、AE=CD.(2)、若AC=12cm,求BD的长.23. 某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵 两次共花费940元 两次购进的A、B两种花草价格均分别相同 .(1)、A、B两种花草每棵的价格分别是多少元?(2)、若再次购买A、B两种花草共12棵 、B两种花草价格不变 ,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.24. 如图 ,已知等腰 在平面直角坐标系中,顶点A在y轴上,直角顶点B在x轴上,点C的坐标为 ,直线 的解析式为 . (1)、求直线 的函数解析式.(2)、如图 ,直线 交y轴于E,延长 至点D,使 ,连结 ,求证: .
(1)、求直线 的函数解析式.(2)、如图 ,直线 交y轴于E,延长 至点D,使 ,连结 ,求证: .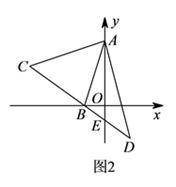 (3)、如图 ,直线 交x轴于M,已知点N的坐标为 ,在直线 上是否存在一点P,使△PBN的面积是△BCM的面积的 ,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)、如图 ,直线 交x轴于M,已知点N的坐标为 ,在直线 上是否存在一点P,使△PBN的面积是△BCM的面积的 ,若存在,请求出点P的坐标;若不存在,请说明理由.