浙江省杭州市2020-2021学年八年级上学期数学期末适应性卷

试卷更新日期：2021-01-20 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，有10小题，共30分）

1. 若一个三角形的两边长分别为2和4，则第三边长可能是（）.

A、1 B、2 C、3 D、7

查看试题解析
2. 下列图形中，是轴对称图形但不是中心对称图形的是（　　）

A、平行四边形 B、等腰三角形 C、矩形 D、正方形

查看试题解析
3. 在下列命题中，为真命题的是（）

A、相等的角是对顶角 B、平行于同一条直线的两条直线互相平行 C、同旁内角互补 D、垂直于同一条直线的两条直线互相平行

查看试题解析
4. 如图，小球起始时位于 $(3 ， 0)$ 处，沿所示的方向击球，小球运动的轨迹如图所示.如果小球起始时位于 $(1 ， 0)$ 处，仍按原来方向击球，小球第一次碰到球桌边时，小球的位置是 $(0 ， 1)$ ，那么小球第2020次碰到球桌边时，小球的位置是（）

A、 $(3 ， 4)$ B、 $(5 ， 4)$ C、 $(7 ， 0)$ D、 $(8 ， 1)$

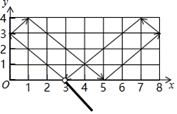查看试题解析

5. 某品牌热水壶的成本为50元，销售商对其销量与定价的关系进行了调查，结果如下：

定价/元	70	80	90	100	110	120
销量/把	80	100	110	100	80	60

现销售了 $105$ 把水壶，则定价约为（）

A、

115

元 B、

105

元 C、

95

元 D、

85

元

查看试题解析

6. 已知关于x的方程 $9 x - 3 = k x + 14$ 有整数解，且关于x的不等式组 ${\begin{array}{l} \frac{x + 15}{2} > x + 5 \\ \frac{2 x}{2} \geq \frac{k - 2}{8} - 2 x \end{array}$ 有且只有4个整数解，则不满足条件的整数k为（）.

A、 $- 8$ B、8 C、10 D、26

查看试题解析
7. 如图， $∠ A = 40 °$ ， $A D$ 垂直平分线段 $B C$ 于点D， $∠ A B C$ 的平分线交 $A D$ 于点E，连接 $E C$ ，则 $∠ C$ 等于（）

A、 $25 °$ B、 $40 °$ C、 $50 °$ D、 $55 °$

查看试题解析
8. 如图，锐角△ABC中，D、E分别是AB、AC边上的点，△ADC≌△ADC′，△AEB≌△AEB′，且 $C^{'} D / / E B^{'} / / B C$ ，BE、CD交于点F.若∠BAC=40°，则∠BFC的大小是（）

A、105° B、110° C、100° D、120°

查看试题解析
9. 如图，已知△ABC的三个顶点A(a，0)、B(b，0)、C(0，2a)(b＞a＞0)，作△ABC关于直线AC的对称图形△AB₁C，若点B₁恰好落在y轴上，则 $\frac{a}{b}$ 的值为(　　)

A、 $\frac{1}{3}$ B、 $\frac{4}{9}$ C、 $\frac{1}{2}$ D、 $\frac{3}{8}$

查看试题解析
10. 甲、乙两车从A地出发，匀速驶往B地.乙车出发1h后，甲车才沿相同的路线开始行驶.甲车先到达B地并停留30分钟后，又以原速按原路线返回，直至与乙车相遇.图中的折线段表示从开始到相遇止，两车之间的距离y（ $k m$ ）与甲车行驶的时间x（h）的函数关系的图象，则（　　）

A、甲车的速度是120 $k m$ / $h$ B、A， B两地的距离是360 $k m$ C、乙车出发4.5h时甲车到达B地 D、甲车出发4.5h最终与乙车相遇

查看试题解析

二、填空题（每小题4分，共6小题，共24分）

11. 如图，在△ABC中，已知BC=5， $S_{△ A B C} = 6$ ，∠C=30°，EF 垂直平分BC，点 P 为直线EF上一动点，则 AP+BP 的最小值是.

查看试题解析
12. 如图是放在地面上的一个长方体盒子，其中AB＝24cm，BC＝12cm，BF＝7cm，点M在棱AB上，且AM＝6cm，点N是FG的中点，一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N，它需要爬行的最短路程为.

查看试题解析
13. 已知△ABC≌△DEF，△ABC的三边分别为3，m，n，△DEF的三边分别为5，p，q.若△ABC的三边均为整数，则m+n+p+q的最大值为.

查看试题解析
14. 关于x，y的二元一次方程组 ${\begin{cases} 2 x + y = - 3 m + 2 \\ x + 2 y = 4 \end{cases}$ 的解满足x+y＞﹣1，则m的取值范围是.

查看试题解析
15. 已知Q在直线 $y = - x + 4$ 上，且点Q到两坐标轴的距离相等，那么点Q的坐标为.

查看试题解析
16. 已知点A，B的坐标分别为(2，0)，(2，4)，以A，B，P为顶点的三角形与 $△ A B O$ 全等，点P与点O不重合，写出符合条件的点P的坐标：．

查看试题解析

三、解答题（共7小题，共66分）

17. 解下列不等式：

(1)、 $3 (1 - x) \geq 2 (x + 9)$ ；

(2)、 $1 - \frac{2 - 3 x}{5} > \frac{1 + x}{2}$ .

查看试题解析
18. 如图，已知 $△ A B C$ ， $A C = B C$ ， $∠ A C B = 90 °$ .

(1)、用直尺和圆规按下列要求作图：（保留作图痕迹，用黑色签字笔加粗加黑）
作 $△ A B C$ 的角平分线 $B D$ 交 $A C$ 于D；
过A点作 $A E$ 垂直于 $B D$ ，垂足为E， $A E$ 交 $B C$ 的延长线于点F；

(2)、证明： $B D = 2 A E$ .

查看试题解析
19. 如图， $△ A B C ≌ △ D E B$ ，点E在 $A B$ 上， $D E$ 与 $A C$ 相交于点F，若 $D E = 7$ ， $B C = 4$ ， $∠ D = 35 °$ ， $∠ C = 60 °$ .

(1)、求线段 $A E$ 的长；

(2)、求 $∠ D F A$ 的度数.

查看试题解析
20. 如图，在四边形 $A B C D$ 中， $A C ⊥ C D ， Δ A D C$ 的面积是 $30 c m^{2} ， D C = 12 c m ， A B = 3 c m ， B C = 4 c m ，$

(1)、求 $A D$ 的长；

(2)、求 $Δ A B C$ 的面积.

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $A D // B C$ ， $∠ A = 90 °$ ， $B D = B C$ ， $C E ⊥ B D$ 于E.

(1)、求证： $△ A B D$ ≌ $△ E C B$ ；

(2)、若 $∠ D C E = 15 °$ ， $A B = 2$ ，求 $B C$ 的长.

查看试题解析
22. 某体育拓展中心的门票每张10元，一次性使用考虑到人们的不同需求，也为了吸引更多的顾客，该拓展中心除保留原来的售票方法外，还推出了一种“购买个人年票”（个人年票从购买日起，可供持票者使用一年）的售票方法.年票分A、B两类：A类年票每张120元，持票者可不限次进入中心，且无需再购买门票；B类年票每张60元，持票者进入中心时，需再购买门票，每次2元.

(1)、小丽计划在一年中花费80元在该中心的门票上，如果只能选择一种购买门票的方式，她怎样购票比较合算？

(2)、小亮每年进入该中心的次数约20次，他采取哪种购票方式比较合算？

(3)、小明根据自己进入拓展中心的次数，购买了A类年票，请问他一年中进入该中心不低于多少次？

查看试题解析
23. 已知一次函数y＝kx－b的图象与x轴、y轴分别相交于点A（2，0）、B（0，-4），点P在该函数的图象上，P到x轴、y轴的距离分别为d₁、d₂.

(1)、求k和b的值；

(2)、当P为线段AB的中点时， d₁+d₂=；

(3)、直接写出d₁+d₂的范围，并求当d₁+d₂＝3时点P的坐标；

(4)、若在线段AB上存在无数个P点，使d₁+md₂＝4（m为常数），求m的值.

查看试题解析