浙江省绍兴市越城区2021届九年级上学期数学期末考试卷

试卷更新日期：2021-01-20 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共40.0分）

1. 二次函数 $y = {(x - 1)}^{2} - 3$ 的最小值是（）

A、2 B、1 C、 $- 2$ D、 $- 3$

查看试题解析
2. 如果 $\frac{a}{b} = 2$ ，则 $\frac{a + b}{a - b}$ 的值是（）

A、3 B、 $- 3$ C、 $\frac{1}{2}$ D、 $\frac{3}{2}$

查看试题解析
3. 在 $R t △ A C B$ 中， $∠ C = 90 °$ ， $A B = 10$ ， $s i n A = \frac{3}{5}$ ， $c o s A = \frac{4}{5}$ ， $t a n A = \frac{3}{4}$ ，则BC的长为（）

A、6 B、 $7.5$ C、8 D、 $12.5$

查看试题解析
4. 如图，四边形ABCD是 $⊙ O$ 的内接四边形，若 $∠ D = 3 ∠ B$ ，则 $∠ B$ 等于（）

A、 $30 °$ B、 $36 °$ C、 $45 °$ D、 $60 °$

查看试题解析
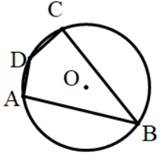5. 在一个不透明的袋子里装有5个红球和若干个白球，它们除颜色外其余完全相同，通过多次摸球试验后发现，摸到红球的频率稳定在 $0.2$ 附近，则估计袋中的白球大约有（）

A、25 B、20 C、15 D、10

查看试题解析
6. 一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米，木工要以一根长为60厘米的木条为一边，做一个与模型三角形相似的三角形，那么另两条边的木条长度不符合条件的是（）

A、30厘米、45厘米 B、40厘米、80厘米 C、80厘米、120厘米 D、90厘米、120厘米

查看试题解析
7. 抛物线 $y = x^{2} - 2$ 与y轴交点的坐标是（）

A、 $(0 ， 2)$ B、 $(0 ， - 2)$ C、 $(2 ， 0)$ D、 $(- 2 ， 0)$

查看试题解析
8. 如图所示，等腰直角三角形ABC与等腰直角三角形 $A' B' C'$ 是位似图形，位似中心为点O，位似比1：2，点A的坐标为 $(1 ， 0)$ ，点C的坐标为 $(0 ， 1)$ ，则点 $B'$ 的坐标为（）

A、 $(2 ， 2)$ B、 $(- 2 ， 2)$ C、 $(- 2 ， - 2)$ D、 $(2 ， 2)$ 或 $(- 2 ， - 2)$

查看试题解析
9. 如图，将 $⊙ O$ 沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧 $\overset{⌢}{A M B}$ 上一点，则 $∠ A P B$ 的度数为 $($ $)$

A、 $60 °$ B、 $30 °$ C、 $75 °$ D、 $45 °$

查看试题解析
10. 把 $(+ 3) - (+ 5) - (- 1) + (- 7)$ 写成省略括号的和的形式是（）

A、 $- 3 - 5 + 1 - 7$ B、 $3 - 5 - 1 - 7$ C、 $3 - 5 + 1 - 7$ D、 $3 + 5 + 1 - 7$

查看试题解析

二、填空题（本大题共6小题，共30.0分）

11. 八边形的内角和度数为 $°$ .

查看试题解析
12. 如果两个相似三角形的面积比为4：9，较小三角形的周长为4，那么这两个三角形的周长和为.

查看试题解析
13. 如图， $△ A B C$ 的顶点都是正方形网格中的格点，则 $tan ∠ A B C =$ .

查看试题解析

14. 如下框内是“已知一条直角边和斜边作直角三角形”的尺规作图过程.

已知：线段a、b，

求作： $R t △ A B C .$ 使得斜边 $A B = b$ ， $A C = a$ .

作法：如图.

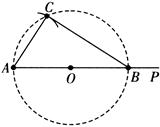
$(1)$ 作射线AP，截取线段 $A B = b$ ；

$(2)$ 以AB为直径，作 $⊙ O$ ；

$(3)$ 以点A为圆心，a的长为半径作弧交 $⊙ O$ 于点C；

$(4)$ 连接AC、CB.

$△ A B C$ 即为所求作的直角三角形.

请您写出上述尺规作图的依据：.

查看试题解析

15. 抛物线 $y = x^{2} - 1$ 与y轴的交点坐标为，与x轴的交点坐标为.

查看试题解析
16. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $c o s B = \frac{2}{3}$ ，把这个直角三角形绕顶点C旋转后得到 $R t △ F E C$ ，其中点E正好落在AB上，EF与AC相交于点D，那么 $\frac{A E}{E B} =$ ， $\frac{A D}{F D} =$ .

查看试题解析

三、计算题（本大题共1小题，共8.0分）

17. 计算： $s i n 30 ° + {tan}^{2} 60 ° - \sqrt{2} c o s 45 °$ .

查看试题解析

四、解答题（本大题共7小题，共72.0分）

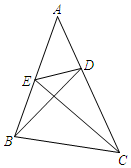
18. 已知二次函数 $y = - x^{2} + 2 x + 3$ .

(1)、求它的顶点坐标和对称轴；

(2)、求它与坐标轴的交点坐标.

查看试题解析
19. 已知：在 $△ A B C$ 中，点D、E分别在AC、AB上，且满足 $∠ A B D = ∠ A C E$ ，求证： $A D \cdot C E = A E \cdot B D$ .

查看试题解析
20. 经过设有交通指示灯的路口时可能遇到红灯，也可能遇到黄灯或绿灯，假设这三种可能性相同.现小亮要连续通过前方的两个设有交通指示灯且运转正常的路口，请用列表法或画树状图法，求小亮至少遇到一次绿灯的概率.

查看试题解析
21. 如图，在某校图书馆门前一段笔直的内部道路AB上，过往车辆限速3米 $/$ 秒在点B的正上方距其7米高的C处有一个探测仪.一辆轿车从点A匀速向点B行驶5秒后此轿车到达D点，探测仪测得 $∠ C A B = 18 °$ ， $∠ C D B = 45 °$ ，求AD之间的距离，并判断此轿车是否超速， $($ 结果精确到 $0.01$ 米 $)$ 【参考数据： $s i n l 8 ° = 0.309$ ， $c o s l 8 ° = 0.951$ ， $t a n l 8 ° = 0.325$ 】

查看试题解析
22.

(1)、问题提出
如图1，在 $△ A B C$ 中， $∠ A = 75 °$ ， $∠ C = 60 °$ ， $A C = 6 \sqrt{2}$ ，求 $△ A B C$ 的外接圆半径R的值；

(2)、问题探究
如图2，在 $△ A B C$ 中， $∠ B A C = 60 °$ ， $∠ C = 45 °$ ， $A C = 8 \sqrt{6}$ ，点D为边BC上的动点，连接AD以AD为直径作 $⊙ O$ 交边AB、AC分别于点E、F，接E、F，求EF的最小值；

(3)、问题解决
如图3，在四边形ABCD中， $∠ B A D = 90 °$ ， $∠ B C D = 30 °$ ， $A B = A D$ ， $B C + C D = 12 \sqrt{3}$ ，连接AC，线段AC的长是否存在最小值，若存在，求最小值：若不存在，请说明理由.

查看试题解析
23. 已知在 $△ A B C$ 中， $C A = C B$ ，在 $△ A E D$ 中， $D A = D E$ ， $∠ A C B = ∠ A D E$ ， $△ A E D$ 绕点A旋转运动如图所示的位置.

(1)、如图1，若 $∠ A C B = 120 °$ ，求证： $△ C A D$ ∽ $△ B A E$ ；

(2)、如图2，若 $∠ A C B = ∠ A D E = 2 α (0 ° < α < 90 °)$ ，探究线段CD与BE的数量关系 $($ 用含 $α$ 的式子表示 $)$ ，并加以证明.

查看试题解析
24. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c$ 与x轴交于 $A (- 2 ， 0)$ ， $B (8 ， 0)$ 两点，与y轴交于点C，且 $O C = 2 O A$ ，抛物线的对称轴与x轴交于点D.

(1)、求抛物线的解析式；

(2)、点P是第一象限内抛物线上位于对称轴右侧的一个动点，设点P点的横坐标为m，且 $S_{△ C D P} = \frac{11}{20} S_{△ A B C}$ ，求m的值；

查看试题解析