山东省潍坊市2020-2021学年高一上学期数学阶段性调研测试试卷
试卷更新日期:2021-01-20 类型:月考试卷
一、单选题
-
1. 已知集合 , ,则 ( ).A、 B、 C、 D、2. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,3. 已知 , ,则 ( )A、 B、 C、 D、4. 函数 的图象大致为( )A、
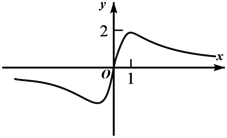 B、
B、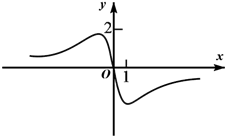 C、
C、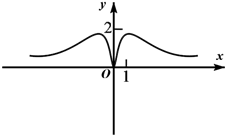 D、
D、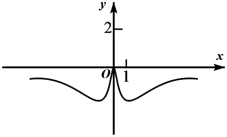 5. 若直角三角形的面积为50,则两条直角边的和的最小值是( )A、 B、 C、10 D、206. 设 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件7. 已知函数 满足 ,且 ,则 ( )A、16 B、8 C、6 D、28. Logistic模型是常用数学模型之一,可应用于流行病学领城,有学者根据公布数据建立了某 地区新冠肺炎累计确诊病例数 ( 的单位:天)的Logistic模型: ,其中 为最大确诊病例数.当 时,标志着已初步遏制疫情,则 约为( )
5. 若直角三角形的面积为50,则两条直角边的和的最小值是( )A、 B、 C、10 D、206. 设 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件7. 已知函数 满足 ,且 ,则 ( )A、16 B、8 C、6 D、28. Logistic模型是常用数学模型之一,可应用于流行病学领城,有学者根据公布数据建立了某 地区新冠肺炎累计确诊病例数 ( 的单位:天)的Logistic模型: ,其中 为最大确诊病例数.当 时,标志着已初步遏制疫情,则 约为( )(注: 为自然对数的底数, )
A、60 B、62 C、66 D、69二、多选题
-
9. 下列四个函数中为减函数的是( )A、 B、 C、 D、10. 已知 , , , ,则下列命题正确的是( )A、若 , ,则 B、若 , ,则 C、若 ,则 D、若 ,则11. 已知 , ,且 ,则( )A、 B、 C、 D、12. 取整函数: 不超过 的最大整数,如 , , .以下关于“取整函数”的性质叙述正确的有( )A、 , B、 , , ,则 C、 , , D、 ,
三、填空题
-
13. 函数 的定义域是.14. 海伦公式亦叫海伦-秦九韶公式,相传这个公式最早是由古希腊数学家阿基米德得出的,而因为这个公式最早出现在海伦的著作《测地术》中,所以被称为海伦公式,它是利用三角形的三条边的边长直接求三角形面积的公式,表达式为 ,其中 , , 分别是三角形的三边长, .已知一根长为10的木棍,截成三段构成一个三角形,若其中有一段的长度为2,则该三角形面积的最大值为.15. 已知 ,若 , ,则 .16. 函数 的部分对应值如下表所示,对于任意 ,点 都在函数 的图象上.已知 ,则 的值是 , 的值是.
x
1
2
3
4
3
1
2
4
四、解答题
-
17. 求下列各式的值(1)、 ;(2)、 .18. 设不等式 的解集为 ,关于 的不等式 的解集为 .(1)、求集合 ;(2)、条件 : ,条件 : , 是 的充分条件,求实数 的取值范围.19. 已知集合 ,函数 .(1)、若 ,且对于任意实数 ,均有 成立,求 , 的值;(2)、 ,若 ,求 , 的值.20. 某品牌饮料原来每瓶成本为10元,售价为15元,月销售8万瓶.(1)、据市场调查,若售价每提高1元,月销售量将相应减少2000瓶,要使月总利润不低于原来的月总利润(月总利润=月销售总收入-月总成本),该饮料每瓶售价最多为多少元?(2)、为提高月总利润,厂家决定下月进行营销策略改革,计划每瓶售价 元,并投入 万元作为营销策略改革费用.据市场调查,每瓶售价每提高1元,月销售量将相应减少 万瓶,则当每瓶售价 为多少时,下月的月总利润最大?并求出下月最大总利润.