浙江省宁波市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-01-20 类型:期末考试
一、选择题
-
1. 下列数对中,在第一象限的点是 ( )A、(1,-3) B、(4,4) C、(-2,-3) D、(-3,0)2. 下列说法错误的是( )A、若三角形一个外角的平分线平行于第三边,则这个三角形一定是等腰三角形 B、有一个角为60°的等腰三角形是等边三角形 C、已知a,b,c是△ABC的三边长,且满足a∶b∶c=3∶3∶4,则△ABC是等腰三角形 D、有两个角不相等的三角形不是等腰三角形3. 下列说法中,错误的一项是( )A、由a(m2+1)< b(m2+1)成立可推a<b成立 B、由a(m2-1)< b(m2-1)成立可推a<b成立 C、由a(m+1) 2< b(m+1) 2成立可推a<b成立 D、由a(m+b)<b(m+a)成立可推am<bm成立4. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、
 B、
B、  C、
C、  D、
D、  5. 如图,在ΔABC中,AD是角平分线,DE⊥AB于点E , ΔABC的面积为10,AB=6,DE=2,则AC的长是( )
5. 如图,在ΔABC中,AD是角平分线,DE⊥AB于点E , ΔABC的面积为10,AB=6,DE=2,则AC的长是( )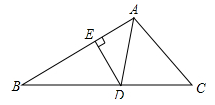 A、6 B、5 C、4 D、36. 下列各组中,能够构成三角形的是( )A、2,3,6 B、2,6,8 C、4,4,10 D、4,5,87. 能说明“锐角 ,锐角 的和是锐角”是假命题的例证图是( ).A、
A、6 B、5 C、4 D、36. 下列各组中,能够构成三角形的是( )A、2,3,6 B、2,6,8 C、4,4,10 D、4,5,87. 能说明“锐角 ,锐角 的和是锐角”是假命题的例证图是( ).A、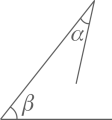 B、
B、 C、
C、 D、
D、 8. 已知正比例函数 ,且y随x的增大而减少,则直线 的图像是( )A、
8. 已知正比例函数 ,且y随x的增大而减少,则直线 的图像是( )A、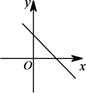 B、
B、 C、
C、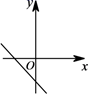 D、
D、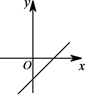 9. 在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
9. 在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( ) A、小莹的速度随时间的增大而增大 B、小梅的平均速度比小莹的平均速度大 C、在起跑后180秒时,两人相遇 D、在起跑后50秒时,小梅在小莹的前面10. 如图,在梯形ABCD中,AB=BC=10cm,CD=6cm,∠C=∠D-90°,动点P、Q同时以每秒1cm的速度从点B出发,点P沿BA、AD、DC运动,点Q沿BC、CD运动,P点与Q点相遇时停止,设P、Q同时从点B出发x秒时,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x之间的函微关系的大致图象为( )
A、小莹的速度随时间的增大而增大 B、小梅的平均速度比小莹的平均速度大 C、在起跑后180秒时,两人相遇 D、在起跑后50秒时,小梅在小莹的前面10. 如图,在梯形ABCD中,AB=BC=10cm,CD=6cm,∠C=∠D-90°,动点P、Q同时以每秒1cm的速度从点B出发,点P沿BA、AD、DC运动,点Q沿BC、CD运动,P点与Q点相遇时停止,设P、Q同时从点B出发x秒时,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x之间的函微关系的大致图象为( ) A、
A、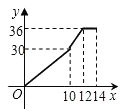 B、
B、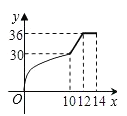 C、
C、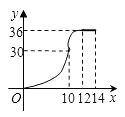 D、
D、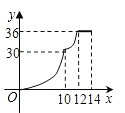
二、填空题
-
11. 命题“同位角相等,两直线平行”的结论。12. 将长为30cm,宽为10cm的长方形白纸,按如图所示的方发粘合起来,粘合部分的宽为3cm.设x张白纸粘合后的总长度为ycm,则y与x的函数关系式.
 13. 如图,在△ABC中,∠A=20°,∠ABC与∠ACB的平分线交于点D1 , ∠ABD1与∠ACD1的平分线交于点D2 , 以此类推,∠ABD2与∠ACD2的平分线交于点D , 则∠BDC的度数是 .
13. 如图,在△ABC中,∠A=20°,∠ABC与∠ACB的平分线交于点D1 , ∠ABD1与∠ACD1的平分线交于点D2 , 以此类推,∠ABD2与∠ACD2的平分线交于点D , 则∠BDC的度数是 .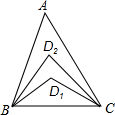 14. 若点A(-5,y1),B(-2,y2)都在一次函数 的图像上,则y1y2(填“>”或“<”).15. 如图,在∠AOB 的边 OA、OB 上取点 M、N,连接 MN,P 是△MON 外角平分线的交点, 若 MN=2, , . 则△MON 的周长是;
14. 若点A(-5,y1),B(-2,y2)都在一次函数 的图像上,则y1y2(填“>”或“<”).15. 如图,在∠AOB 的边 OA、OB 上取点 M、N,连接 MN,P 是△MON 外角平分线的交点, 若 MN=2, , . 则△MON 的周长是;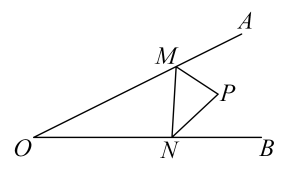 16. 如图,△ABC中,点E是BC上的一点,EC=3BE,点D是AC中点,若S△ABC=36,则S△ADF-S△BEF = .
16. 如图,△ABC中,点E是BC上的一点,EC=3BE,点D是AC中点,若S△ABC=36,则S△ADF-S△BEF = .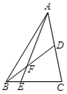
三、解答题
-
17. 解不等式组: ,并在数轴上表示出它的解集.(写出正整数)
 18. 解下列方程:(1)、 ;(2)、 ,19. 如图,在四边形 中, ,点E,F分别在 , 上, , ,求证: .
18. 解下列方程:(1)、 ;(2)、 ,19. 如图,在四边形 中, ,点E,F分别在 , 上, , ,求证: . 20. 如图,A、B、C在同一直线上,且△ABD,△BCE都是等边三角形,AE交BD于点M,CD交BE于点N,MN∥AC,求证:
20. 如图,A、B、C在同一直线上,且△ABD,△BCE都是等边三角形,AE交BD于点M,CD交BE于点N,MN∥AC,求证: (1)、∠BDN=∠BAM;(2)、△BMN是等边三角形.21.(1)、解不等式 ,并把所得解集表示在数轴上.(2)、解不等式组 ,并写出它的所有整数解.22. 某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.
(1)、∠BDN=∠BAM;(2)、△BMN是等边三角形.21.(1)、解不等式 ,并把所得解集表示在数轴上.(2)、解不等式组 ,并写出它的所有整数解.22. 某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.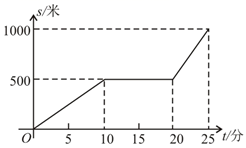 (1)、学校离他家米,从出发到学校,王老师共用了分钟;王老师吃早餐用了分钟?(2)、观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?(3)、求出王老师吃完早餐后的平均速度是多少?23. 如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(-1,a),l1与y轴交于点C,l2与x轴交于点A
(1)、学校离他家米,从出发到学校,王老师共用了分钟;王老师吃早餐用了分钟?(2)、观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?(3)、求出王老师吃完早餐后的平均速度是多少?23. 如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(-1,a),l1与y轴交于点C,l2与x轴交于点A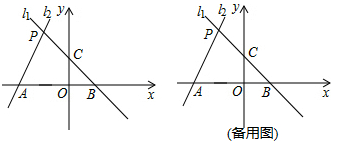 (1)、求a的值及直线l1的解析式。(2)、求四边形PAOC的面积。(3)、在x轴上方有一动直线平行于x轴,分别与l1 , l2交于点M,N,且点M在点N的右侧,x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由。
(1)、求a的值及直线l1的解析式。(2)、求四边形PAOC的面积。(3)、在x轴上方有一动直线平行于x轴,分别与l1 , l2交于点M,N,且点M在点N的右侧,x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由。