江苏省徐州市沛县2019-2020学年八年级下学期数学开学试卷
试卷更新日期:2021-01-20 类型:开学考试
一、单选题
-
1. 下列标志图中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,为必然事件的是A、购买一张彩票,中奖. B、打开电视,正在播放广告. C、抛掷一枚硬币,正面向上. D、一个袋中只装有5个黑球,从中摸出一个球是黑球.3. 要反映台州市某一周每天的最高气温的变化趋势,宜采用( )A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布统计图4. 下列调查中,适宜采用抽样调查方式的是( )A、调查八年级某班学生的视力情况 B、调查乘坐飞机的旅客是否携带违禁物品 C、调查某品牌LED灯的使用寿命 D、学校在给学生订制校服前尺寸大小的调查5. 一个不透明的盒子中装有 个黑球、 个白球,它们除颜色外都相同.若从中任意摸出一个球,摸到哪种颜色的球的可能性最大( )A、黑色 B、白色 C、一样大 D、无法判断6. 如图,为测量池塘边A,B两点的距离,小明在池塘的一侧选取一点O,测得 、 的中点分别是点D,E,且 米,则A、B的距离是( )
2. 下列事件中,为必然事件的是A、购买一张彩票,中奖. B、打开电视,正在播放广告. C、抛掷一枚硬币,正面向上. D、一个袋中只装有5个黑球,从中摸出一个球是黑球.3. 要反映台州市某一周每天的最高气温的变化趋势,宜采用( )A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布统计图4. 下列调查中,适宜采用抽样调查方式的是( )A、调查八年级某班学生的视力情况 B、调查乘坐飞机的旅客是否携带违禁物品 C、调查某品牌LED灯的使用寿命 D、学校在给学生订制校服前尺寸大小的调查5. 一个不透明的盒子中装有 个黑球、 个白球,它们除颜色外都相同.若从中任意摸出一个球,摸到哪种颜色的球的可能性最大( )A、黑色 B、白色 C、一样大 D、无法判断6. 如图,为测量池塘边A,B两点的距离,小明在池塘的一侧选取一点O,测得 、 的中点分别是点D,E,且 米,则A、B的距离是( ) A、16米 B、18米 C、20米 D、22米7. 菱形具有而矩形不具有的性质是( )A、对边相等 B、对角线互相平分 C、对角线互相垂直 D、对角线相等8. 如图,矩形 中, , ,点P从点B出发,沿 向终点D匀速运动.设点P走过的路程为x, 的面积为S,能正确反映S与x之间函数关系的图象是( )
A、16米 B、18米 C、20米 D、22米7. 菱形具有而矩形不具有的性质是( )A、对边相等 B、对角线互相平分 C、对角线互相垂直 D、对角线相等8. 如图,矩形 中, , ,点P从点B出发,沿 向终点D匀速运动.设点P走过的路程为x, 的面积为S,能正确反映S与x之间函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 在整数 中,数字“0”出现的频率是.10. 在平面直角坐标系中,点 到原点的距离是.11. 已知,在▱ABCD中,∠A= ∠B,则∠A= .12. 一个不透明的口袋中装有 个白色球, 个红色球, 个黄色球,这些球除颜色外均相同,搅匀后随机从袋中摸出 个球是白色球的概率是.13. 若函数 的图象如图所示,则关于x的不等式 的解集是.
 14. 如图,在□ 中, ⊥ 于点 , ⊥ 于点 .若 , ,且□ 的周长为40,则□ 的面积为。
14. 如图,在□ 中, ⊥ 于点 , ⊥ 于点 .若 , ,且□ 的周长为40,则□ 的面积为。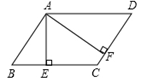 15. 如图,在 中, , , ,P为边 上一动点, 于E, 于F,则 的最小值为.
15. 如图,在 中, , , ,P为边 上一动点, 于E, 于F,则 的最小值为.
三、解答题
-
16. 求下列各式中的x:(1)、(2)、17. 在一个不透明的口袋里装有若干个质地相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,多次重复摸球.下表是多次活动汇总后统计的数据:
摸球的次数S
150
200
500
900
1000
1200
摸到白球的频数n
51
64
156
275
303
361
摸到白球的频率
0.34
0.32
0.312
0.306
0303
0.301
(1)、请估计:当次数S很大时,摸到白球的频率将会接近;假如你去摸一次,你摸到红球的概率是(精确到0.1).(2)、试估算口袋中红球有多少只?18. 为做好食堂的服务工作,某学校食堂对学生最喜爱的菜肴进行了抽样调查,下面试根据收集的数据绘制的统计图(不完整): (1)、参加抽样调查的学生数是人,扇形统计图中“大排”部分的圆心角是°;
(1)、参加抽样调查的学生数是人,扇形统计图中“大排”部分的圆心角是°;
(2)、把条形统计图补充完整;(3)、若全校有3000名学生,请你根据以上数据估计最喜爱“烤肠”的学生人数.
19.方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
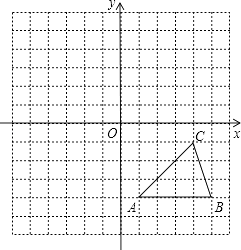 (1)、试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;(2)、以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标.20. 已知:如图, , ,垂足分别为D、C,且 , ,求证:
(1)、试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;(2)、以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标.20. 已知:如图, , ,垂足分别为D、C,且 , ,求证: 21. 已知:如图,在四边形ABCD中,AB=CD,BC=AD,点E,F在AC上,且AF=CE.求证:四边形BEDF是平行四边形.
21. 已知:如图,在四边形ABCD中,AB=CD,BC=AD,点E,F在AC上,且AF=CE.求证:四边形BEDF是平行四边形. 22. 如图, 的四个内角的平分线分别相交于点E、F、G、H,四边形 是怎样的特殊四边形?证明你的结论.
22. 如图, 的四个内角的平分线分别相交于点E、F、G、H,四边形 是怎样的特殊四边形?证明你的结论. 23. 如图,菱形 的周长为 cm,对角线 、 相交于点O, cm,求对角线 的长和菱形 的面积.
23. 如图,菱形 的周长为 cm,对角线 、 相交于点O, cm,求对角线 的长和菱形 的面积. 24. 如图,四边形ABCD是正方形,△EBC是等边三角形.
24. 如图,四边形ABCD是正方形,△EBC是等边三角形. (1)、求证:△ABE≌△DCE;(2)、求∠AED的度数.25. 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
(1)、求证:△ABE≌△DCE;(2)、求∠AED的度数.25. 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒. (1)、△ODP的面积S= .(2)、t为何值时,四边形PODB是平行四边形?(3)、在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;(4)、若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
(1)、△ODP的面积S= .(2)、t为何值时,四边形PODB是平行四边形?(3)、在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;(4)、若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)