浙江省杭州市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-01-20 类型：期末考试

进入出卷网下载

一、单选题

1. 一个布袋里装有2个红球、3个黄球和5个白球，除颜色外其它都相同.搅匀后任意摸出一个球，是黄球的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{10}$ C、 $\frac{1}{5}$ D、 $\frac{7}{10}$

查看试题解析
2. AB和CD是⊙O的两条平行弦，AB＝6，CD＝8，⊙O的半径为5，则AB与CD间的距离为（）

A、1或7 B、7 C、1 D、3或4

查看试题解析
3. 设y＝y₁﹣y₂ ， y₁与x成正比例，y₂与x²成正比例，则y与x的函数关系是（）

A、正比例函数 B、一次函数 C、二次函数 D、以上均不正确

查看试题解析
4. 函数y=﹣2x²先向右平移1个单位，再向下平移2个单位，所得函数解析式是（）

A、y=﹣2（x﹣1）²+2 B、y=﹣2（x﹣1）²﹣2 C、y=﹣2（x+1）²+2 D、y=﹣2（x+1）²﹣2

查看试题解析
5. 若 $\frac{x}{y} = \frac{2}{5}$ ，则 $\frac{x + y}{y}$ 的值为（）

A、 $\frac{2}{5}$ B、 $\frac{7}{2}$ C、 $\frac{5}{7}$ D、 $\frac{7}{5}$

查看试题解析
6. 如图，△ABC内接于⊙O，BD是⊙O的直径.若∠DBC＝33°，则∠A等于（）

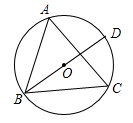A、33° B、57° C、67° D、66°

查看试题解析
7. 已知二次函数 $y = - x^{2} + 2 x + 4$ ，则下列关于这个函数图象和性质的说法，正确的是（）

A、图象的开口向上 B、图象的顶点坐标是 $(1, 3)$ C、当 $x < 1$ 时，y随x的增大而增大 D、图象与x轴有唯一交点

查看试题解析
8. 用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.9，下列说法正确的是（）

A、种植10棵幼树，结果一定是“有9棵幼树成活” B、种植100棵幼树，结果一定是“90棵幼树成活”和“10棵幼树不成活” C、种植10n棵幼树，恰好有“n棵幼树不成活” D、种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.9

查看试题解析
9. 如图，等腰直角三角形ABC，∠BAC＝90°，D、E是BC上的两点，且BD＝CE，过D、E作DM、EN分别垂直AB、AC，垂足为M、N，交于点F，连接AD、AE.其中①四边形AMFN是正方形；②△ABE≌△ACD；③CE²+BD²＝DE²；④当∠DAE＝45°时，AD²＝DE•CD.正确结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，直线l₁：y=x+1与直线 $l_{2} ： y = \frac{1}{2} x + \frac{1}{2}$ 相交于点P（﹣1，0）.直线l₁与y轴交于点A.一动点C从点A出发，先沿平行于x轴的方向运动，到达直线l₂上的点B₁处后，改为垂直于x轴的方向运动，到达直线l₁上的点A₁处后，再沿平行于x轴的方向运动，到达直线l₂上的点B₂处后，又改为垂直于x轴的方向运动，到达直线l₁上的点A₂处后，仍沿平行于x轴的方向运动，…照此规律运动，动点C依次经过点B₁ ， A₁ ， B₂ ， A₂ ， B₃ ， A₃ ， …，B₂₀₁₄ ， A₂₀₁₄ ， …则当动点C到达A₂₀₁₄处时，运动的总路径的长为（）

A、2014² B、2²⁰¹⁵-2 C、2²⁰¹³+1 D、2²⁰¹⁴-1

查看试题解析

二、填空题

11. 两个相似三角形的面积比为4：9，那么它们对应中线的比为．

查看试题解析
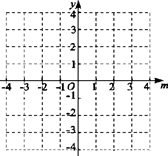
12. 如图，AB是半圆的直径，O是圆心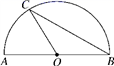， $\hat{B C} = 2 \hat{A C}$ ，则∠ABC＝°.

查看试题解析
13. 如图，已知点A（2，1），B（0，2），将线段AB绕点M逆时针旋转到A₁B₁ ，点A与A₁是对应点，则点M的坐标是.

查看试题解析
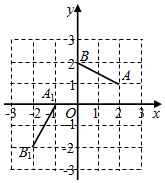14. 如图，点G是△ABC的重心，过点G作GE//BC，交AC于点E，连结GC. 若△ABC的面积为1，则△GEC的面积为.

查看试题解析
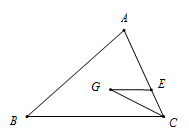15. 如图，抛物线y＝﹣x²+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B.
①抛物线y＝﹣x²+2x+m+1与直线y＝m+2有且只有一个交点；

②若点M（﹣2，y₁）、点N（ $\frac{1}{2}$ ，y₂）、点P（2，y₃）在该函数图象上，则y₁＜y₂＜y₃；

③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）²+m；

④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为 $\sqrt{34} + \sqrt{2}$ .

其中正确判断的序号是.

查看试题解析

三、解答题

16. 已知 $\frac{a}{b} = \frac{2}{3}$ ，求 $\frac{3 a - 4 b}{2 a + b}$ 的值.

查看试题解析
17. 已知二次函数y₁=ax²＋bx－3的图象经过点A（2，-3），B（-1，0），与y轴交于点C，与x轴另一交点交于点D.

(1)、求二次函数的解析式；

(2)、求点C、点D的坐标；

(3)、若一条直线y₂_，经过C、D两点，请直接写出y₁＞y₂时，x的取值范围.

查看试题解析
18. 在一次数学活动课上，小芳到操场上测量旗杆的高度，她的测量方法是：拿一根高3.5米的竹竿直立在离旗杆27米的C处（如图），然后沿BC方向走到D处，这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上，又测得C、D两点的距离为3米，小芳的目高为1.5米，利用她所测数据，求旗杆的高.

查看试题解析
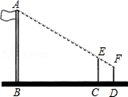19. 把大小和形状完全相同的6张卡片分成两组，每组3张，分别标上1、2、3，将这两组卡片分别放入两个盒子中搅匀，再从中随机抽取一张．

(1)、试求取出的两张卡片数字之和为奇数的概率；

(2)、若取出的两张卡片数字之和为奇数，则甲胜；取出的两张卡片数字之和为偶数，则乙胜；试分析这个游戏是否公平？请说明理由．

查看试题解析
20. 在数学课上，老师提出利用尺规作图完成下面问题：已知：△ABC是⊙O的内接三角形.求作：△ABC中∠BAC的平分线.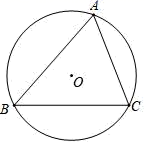

小明的作法如下：
（1）作BC边的垂直平分线DE，交BC于点D，交弧BC于点E；
（2）连接AE，交BC边于点F；则线段AF为所求△ABC中∠BAC的平分线.根据小明设计的尺规作图过程，

①在图中补全图形（尺规作图，保留作图痕迹）；

②完成下面的证明.

证明：∵OB＝OC，DE是线段BC的垂直平分线

∴圆心O在直线DE上（）.

∵DE⊥BC，

∴ $\overset{⌢}{B E} = \overset{⌢}{C E}$ （）.

∴∠BAE＝∠CAE（），
∴线段AF为所求△ABC中∠BAC的平分线.

查看试题解析
21. 某商店经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：

时间 x（天）

1≤x＜50

50≤x≤90

售价（元/件）

x+40

90

每天销量（件）

200﹣2x

已知该商品的进价为每件30元，设销售该商品的每天利润为y元.

(1)、求出y与x的函数关系式；

(2)、问销售该商品第几天时，当天销售利润最大，最大利润是多少？

(3)、在前50天销售过程中，为了给顾客发放福利，每售出一件商品就返还2a元给顾客，且要求售价不低于80元，但是前50天的销售中，仍可以获得最大利润5850元，求出a的值.

查看试题解析
22. 如图，在平面直角坐标系xOy中，O为坐标原点，点A（6，0），点B（0，6），△ABO的中线AC与y轴交于点C，且⊙M经过O，A，C三点.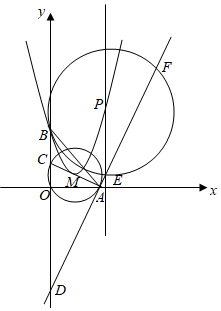

(1)、圆心M的坐标为；

(2)、抛物线经过点B，且以圆心M为顶点，求抛物线的解析式；

(3)、若直线AD与⊙M相切于点A，交y轴于点D，求直线AD的函数表达式；

(4)、若（2）中的抛物线上有一动点P，过点P作PE∥y轴，交（3）中的直线AD于点E.若以PE为半径的⊙P与直线AD相交于另一点F.求EF的最小值.

查看试题解析

时间 x（天）	1≤x＜50	50≤x≤90
售价（元/件）	x+40	90
每天销量（件）	200﹣2x