广西壮族自治区南宁市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-01-20 类型:期末考试
一、单选题
-
1. 的绝对值是( )A、±5 B、 C、5 D、2. 不等式 的解集在数轴上表示为( )A、
 B、
B、 C、
C、 D、
D、 3. 使二次根式 有意义的x的取值范围是( )A、x≠2 B、x>2 C、x≤2 D、x≥24. 据《南宁晚报》报道,2020年的国庆黄金周,南宁的天气格外晴朗、阳光明媚,市民游客都纷纷走出了家门,涌进南宁的各个旅游景区和公园.但是由于今年疫情影响,对于流动人口严格控制,最终,南宁动物园以8.54万人次的游客量,在各景区(公园)的客流榜上遥遥领先.那么8.54万用科学记数法表示是( )A、 B、 C、 D、5. 把分式方程 ,的两边同时乘以x-2,约去分母,得( )A、1-(1-x)=1 B、1+(1-x)=1 C、1-(1-x)=x-2 D、1+(1-x)=x-26. 反比例函数y= 在第一象限的图象如图所示,则k的值可能是( )
3. 使二次根式 有意义的x的取值范围是( )A、x≠2 B、x>2 C、x≤2 D、x≥24. 据《南宁晚报》报道,2020年的国庆黄金周,南宁的天气格外晴朗、阳光明媚,市民游客都纷纷走出了家门,涌进南宁的各个旅游景区和公园.但是由于今年疫情影响,对于流动人口严格控制,最终,南宁动物园以8.54万人次的游客量,在各景区(公园)的客流榜上遥遥领先.那么8.54万用科学记数法表示是( )A、 B、 C、 D、5. 把分式方程 ,的两边同时乘以x-2,约去分母,得( )A、1-(1-x)=1 B、1+(1-x)=1 C、1-(1-x)=x-2 D、1+(1-x)=x-26. 反比例函数y= 在第一象限的图象如图所示,则k的值可能是( ) A、1 B、2 C、3 D、47. 下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )A、 B、 C、 D、8. 在平面直角坐标系中,⊙O的半径为5,圆心在原点O,则P(﹣3,4)与⊙O的位置关系是( )A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定9. 如图,直径AB、CD互相垂直,现有一小球在此圆盘上滚动,落在阴影部分的概率为( )
A、1 B、2 C、3 D、47. 下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )A、 B、 C、 D、8. 在平面直角坐标系中,⊙O的半径为5,圆心在原点O,则P(﹣3,4)与⊙O的位置关系是( )A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定9. 如图,直径AB、CD互相垂直,现有一小球在此圆盘上滚动,落在阴影部分的概率为( )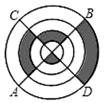 A、 B、 C、 D、10. 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )米
A、 B、 C、 D、10. 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )米 A、5 B、8 C、12 D、1311. 如图,在4×4的正方形网格中,△MNP绕某点旋转90°,得到△M1N1P1 , 则其旋转中心可以是( )
A、5 B、8 C、12 D、1311. 如图,在4×4的正方形网格中,△MNP绕某点旋转90°,得到△M1N1P1 , 则其旋转中心可以是( ) A、点E B、点F C、点G D、点H12. 如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则 与 的弧长之和为( )
A、点E B、点F C、点G D、点H12. 如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则 与 的弧长之和为( )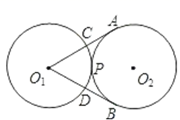 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,在数轴上点A和点B表示的数之间的整数是
 14. 从一副没有“大小王”的扑克牌中随机抽取一张,点数为“ ”的概率是.15. 分解因式: .16. 若关于 的一元二次方程 的一根是0,则 =.17. 一个直角三角形的两条直角边长分别为6cm、8cm,则它的内切圆的半径为cm.18. 如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需个五边形.
14. 从一副没有“大小王”的扑克牌中随机抽取一张,点数为“ ”的概率是.15. 分解因式: .16. 若关于 的一元二次方程 的一根是0,则 =.17. 一个直角三角形的两条直角边长分别为6cm、8cm,则它的内切圆的半径为cm.18. 如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需个五边形.
三、解答题
-
19. 计算:20. 解方程:21. 在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
 (1)、求证:△BEC≌△DEC;(2)、延长BE交AD于F,当∠BED=120°时,求∠EFD的度数.22. 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)、求证:△BEC≌△DEC;(2)、延长BE交AD于F,当∠BED=120°时,求∠EFD的度数.22. 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: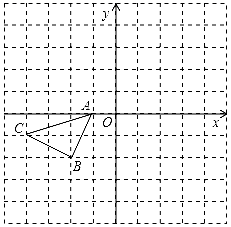
( 1 )以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1 , 画出△AB1C1.
( 2 )作出△ABC关于坐标原点O成中心对称的△A2B2C2.
( 3 )作出点C关于x轴的对称点P.若点P向右平移x(x取整数)个单位长度后落在△A2B2C2的内部,请直接写出x的值.
23. 有一个可自由转动的转盘,被分成了4个相同的扇形,分别标有数1,2,3,4(如图所示),另有一个不透明的口袋装有分别标有数0,1,3的三个小球(除数字不同外,其余都相同),小亮转动一次转盘,停止后指针指向某一扇形(指针指向两个扇形的交线时,当作指向右边的扇形),扇形内的数是小亮的幸运数,小红任意摸出一个小球,小球上的数是小红的吉祥数,然后计算这两个数的积. (1)、请你用画树状图或列表的方法,求这两个数的积为0的概率;(2)、小亮与小红做游戏,规则是:若这两个数的积为奇数,小亮赢;否则,小红赢.你认为该游戏公平吗?为什么?如果不公平,请你修改该游戏规则,使游戏公平.24. 南宁某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.(1)、求平均每次下调的百分率;(2)、某人准备以开盘均价购买一套100平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,送两年物业管理费.物业管理费是每平方米每月1.5元.请问哪种方案更优惠?
(1)、请你用画树状图或列表的方法,求这两个数的积为0的概率;(2)、小亮与小红做游戏,规则是:若这两个数的积为奇数,小亮赢;否则,小红赢.你认为该游戏公平吗?为什么?如果不公平,请你修改该游戏规则,使游戏公平.24. 南宁某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.(1)、求平均每次下调的百分率;(2)、某人准备以开盘均价购买一套100平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,送两年物业管理费.物业管理费是每平方米每月1.5元.请问哪种方案更优惠?