辽宁省鞍山市岫岩县2020-2021学年八年级上学期数学12月月考试卷
试卷更新日期:2021-01-19 类型:月考试卷
一、单选题
-
1. 如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )
 A、2 B、3 C、4 D、52. 正十边形的每一个外角的度数为( )A、 B、 C、 D、3. 下列各运算中,计算正确的是( )A、 B、 C、 D、4. 计算: ( )A、 B、 C、 D、5. 如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P , DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A、2 B、3 C、4 D、52. 正十边形的每一个外角的度数为( )A、 B、 C、 D、3. 下列各运算中,计算正确的是( )A、 B、 C、 D、4. 计算: ( )A、 B、 C、 D、5. 如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P , DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( ) A、3 B、4 C、5 D、66. 如图,已知直线m是正五边形ABCDE的对称轴,连接BD交m于点F,则 的度数为( )
A、3 B、4 C、5 D、66. 如图,已知直线m是正五边形ABCDE的对称轴,连接BD交m于点F,则 的度数为( ) A、 B、 C、 D、7. 如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( )
A、 B、 C、 D、7. 如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( ) A、8 B、7 C、6 D、58. 如图,在 和 中, , , , .连接 、 交于点M,连接 .下列结论:
A、8 B、7 C、6 D、58. 如图,在 和 中, , , , .连接 、 交于点M,连接 .下列结论: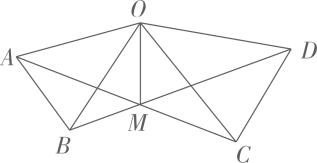
① ;② ;③ 平分 ;④ 平分
其中正确的结论个数有( )个.
A、4 B、3 C、2 D、1二、填空题
-
9. 在平面直角坐标系中,点 关于x轴对称的点的坐标是.10. 计算: 的结果为 .11. 一个三角形的两边长为2和6,第三边为偶数,则这个三角形的周长为12. 若 , ,则代数式 的值等于.13. 已知 , ,则 .14. 如图,已知 中,点D,E分别在边AC,AB上,连接BD,DE, ,请你添加一个条件,使 ,你所添加的条件是.(只填一个条件即可)
 15. 如图,在 中, , , 的平分线 交 于点 , ,交 的延长线于点 ,若 ,则 .16. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则 周长的最小值为.
15. 如图,在 中, , , 的平分线 交 于点 , ,交 的延长线于点 ,若 ,则 .16. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则 周长的最小值为.
三、解答题
-
17. 因式分解:18. 计算:19. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后, 的顶点均在格点上.
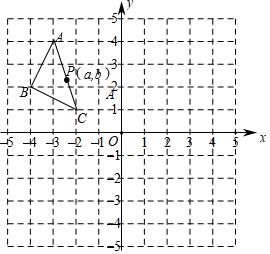 (1)、①将 向下平移5个单位长度,再向右平移1个单位长度后得到对应的 ,画出 ;
(1)、①将 向下平移5个单位长度,再向右平移1个单位长度后得到对应的 ,画出 ;②画出 关于y轴对称的 ;
(2)、 是 的AC边上一点,请直接写出经过上述的两次变换后在 中对应的点 的坐标.20. ,其中 .21. 如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC. (1)、求证:AE=AD;(2)、若∠ACB=65°,求∠BDC的度数.22. 图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形.
(1)、求证:AE=AD;(2)、若∠ACB=65°,求∠BDC的度数.22. 图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形. (1)、用两种不同的方法表示图②中小正方形(阴影部分)的面积:
(1)、用两种不同的方法表示图②中小正方形(阴影部分)的面积:方法一: ;
方法二: .
(2)、(m+n)2 ,(m−n) 2 , mn这三个代数式之间的等量关系为(3)、应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求x−y的值.23. 如图,在 中, 于点D, 于点E,BD、CE相交于点G, , 交AB于点F,连接FG.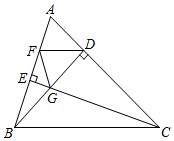
求证:
(1)、 ;(2)、 .24. 如图 (1)、(问题情境)小明遇到这样一个问题:
(1)、(问题情境)小明遇到这样一个问题:如图①,已知 是等边三角形,点 为 边上中点, , 交等边三角形外角平分线 所在的直线于点 ,试探究 与 的数量关系.
小明发现:过 作 ,交 于 ,构造全等三角形,经推理论证问题得到解决.请直接写出 与 的数量关系,并说明理由.
(2)、(类比探究)如图②,当 是线段 上(除 外)任意一点时(其他条件不变)试猜想 与 的数量关系并证明你的结论.
(3)、(拓展应用)当 是线段 上延长线上,且满足 (其他条件不变)时,请判断 的形状,并说明理由.