浙江省杭州市滨江区2020-2021学年七年级上学期数学期末考试卷
试卷更新日期:2021-01-19 类型:期末考试
一、单选题
-
1. 2020的相反数是( )A、 B、 C、-2020 D、20202. 早在两千多年前,中国人就已经开始使用负数,并运用到生产和生活中,比西方早一千多年,下列各式计算结果为负数的是( )A、 B、 C、 D、3. 近年来,国家重视精准扶贫,收效显著.据统计约有65 000 000人脱贫,把65 000 000用科学记数法表示,正确的是( )A、0.65×108 B、6.5×107 C、6.5×108 D、65×1064. 下列说法正确的是( )A、一个数的平方根有两个,它们互为相反数 B、一个数的立方根,不是正数就是负数 C、如果一个数的立方根是这个数本身,那么这个数一定是﹣1,0,1中的一个 D、如果一个数的平方根是这个数本身,那么这个数是1或者05. 下列说法正确的是( )A、0是单项式; B、 的系数是1 C、 是三次二项式 D、 与 是同类项6. 如图,实数﹣3、x、3、y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最小的数对应的点是( )
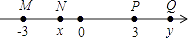 A、点M B、点N C、点P D、点Q7. 下列说法中,正确的是( )A、射线是直线的一半 B、线段AB是点A与点B的距离 C、两点之间所有连线中,线段最短 D、角的大小与角的两边所画的长短有关8. 下列等式变形不正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则9. “某幼儿园给小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则少2个,问苹果有多少个?”若设共有x个苹果,则列出的方程是( )A、 B、 C、 D、10. 已知max 表示取三个数中最大的那个数,例如:当x=9时,max =81.当max 时,则x的值为( )A、 B、 C、 D、
A、点M B、点N C、点P D、点Q7. 下列说法中,正确的是( )A、射线是直线的一半 B、线段AB是点A与点B的距离 C、两点之间所有连线中,线段最短 D、角的大小与角的两边所画的长短有关8. 下列等式变形不正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则9. “某幼儿园给小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则少2个,问苹果有多少个?”若设共有x个苹果,则列出的方程是( )A、 B、 C、 D、10. 已知max 表示取三个数中最大的那个数,例如:当x=9时,max =81.当max 时,则x的值为( )A、 B、 C、 D、二、填空题
-
11. 3.(选填“>”、“<”或“=”)12. 甲、乙两地海拔高度分别为20米和﹣9米,那么甲地比乙地高米.13. 将0.09493用四舍五入法取近似值精确到百分位,其结果是.14. 如图,点C在线段AB的延长线上,BC=2AB,点D是线段AC的中点,AB=4,则BD长度是.
 15. 已知关于x的一元一次方程 的解为 ,那么关于y的一元一次方程 的解为.16. 一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折2次后,可以得3条折痕,那么对折5次可以得到条折痕.
15. 已知关于x的一元一次方程 的解为 ,那么关于y的一元一次方程 的解为.16. 一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折2次后,可以得3条折痕,那么对折5次可以得到条折痕.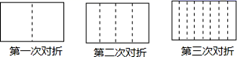
三、解答题
-
17. 计算(1)、3﹣(﹣8)+(﹣5)+6;(2)、﹣12020+24÷ .18. 解方程(1)、(2)、1- =19. 先化简,再求值: 其中20. 某市某公交车从起点到终点共有六个站,一辆公交车由起点开往终点,在起点站始发时上了部分乘客,从第二站开始下车、上车的乘客数如表:
站次
人数
二
三
四
五
六
下车(人)
3
6
10
7
19
上车(人)
12
10
9
4
0
(1)、求本趟公交车在起点站上车的人数;(2)、若公交车的收费标准是上车每人2元,计算此趟公交车从起点到终点的总收入?21. 如图, 为直线 上一点, , 平分 , .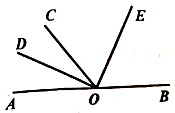 (1)、求 的度数.(2)、试判断 是否平分 ,并说明理由.22. 如图
(1)、求 的度数.(2)、试判断 是否平分 ,并说明理由.22. 如图 (1)、如图,已知点 在线段 上, 分别是 , 的中点,求线段 的长度;(2)、在(1)题中,如果 ,其他条件不变,求此时线段 的长度.23. 某市为鼓励市民节约用水,特制定如下的收费标准:若每月每户用水不超过10立方米,则按3元/立方米的水价收费,并加收0.2元/立方米的污水处理费;若超过10立方米,则超过的部分按4元/立方米的水价收费,污水处理费不变.(1)、若小华家5月份的用水量为8立方米,那么小华家5月份的水费为元;(2)、若小华家6月份的用水量为15立方米,那么小华家6月份的水费为元;(3)、若小华家某个月的用水量为a(a>10)立方米,求小华家这个月的水费(用含a的式子表示).24. 如图,在数轴上 点表示的数是-8, 点表示的数是2.动线段 (点 在点 的右侧),从点 与点 重合的位置出发,以每秒2个单位的速度向右运动,运动时间为 秒.
(1)、如图,已知点 在线段 上, 分别是 , 的中点,求线段 的长度;(2)、在(1)题中,如果 ,其他条件不变,求此时线段 的长度.23. 某市为鼓励市民节约用水,特制定如下的收费标准:若每月每户用水不超过10立方米,则按3元/立方米的水价收费,并加收0.2元/立方米的污水处理费;若超过10立方米,则超过的部分按4元/立方米的水价收费,污水处理费不变.(1)、若小华家5月份的用水量为8立方米,那么小华家5月份的水费为元;(2)、若小华家6月份的用水量为15立方米,那么小华家6月份的水费为元;(3)、若小华家某个月的用水量为a(a>10)立方米,求小华家这个月的水费(用含a的式子表示).24. 如图,在数轴上 点表示的数是-8, 点表示的数是2.动线段 (点 在点 的右侧),从点 与点 重合的位置出发,以每秒2个单位的速度向右运动,运动时间为 秒. (1)、①已知点 表示的数是-6,试求点 表示的数;
(1)、①已知点 表示的数是-6,试求点 表示的数;②用含有 的代数式表示点 表示的数;
(2)、当 时,求 的值.(3)、试问当线段 在什么位置时, 或 的值始终保持不变?请求出它的值并说明此时线段 的位置.