初中数学苏科版七年级下册 8.2 幂的乘方与积的乘方 同步训练
试卷更新日期:2021-01-14 类型:同步测试
一、单选题
-
1. 已知m,n是整数,a≠ 0,b≠ 0,则下列各式中,能表示 “积的乘方法则”的是( )A、anam=an+m B、(a m)n=a mn C、a0=1 D、(ab)n=anbn2. 下列式子中,正确的有( )
①m3∙m5=m15; ②(a3)4=a7; ③(-a2)3=-(a3)2; ④(3x2)2=6x6
A、0个 B、1个 C、2个 D、3个3. 下列计算正确的是( )
A、(x2n)3=x2n+3 B、(a2)3+(a3)2=(a6)2 C、(a2)3+(b2)3=(a+b)6 D、[(-x)2]n=x2n4. 已知23×83=2n , 则n的值是( )A、18 B、8 C、7 D、125. 计算(-a2)3·(-a3)2的结果是( )A、a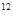 B、-a
B、-a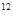 C、-a
D、-a
C、-a
D、-a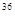 6. 已知: , , 则的值为( )
6. 已知: , , 则的值为( )
A、 B、 C、 D、7. 若3m=5,9n=10,则3m+2n的值是( )A、50 B、500 C、250 D、25008. 已知 、 均为正整数,且 ,则 ( )A、 B、 C、 D、9. 计算( )2020x( )2021=( )A、-1 B、 C、1 D、10. 比较255、344、433的大小( )A、255<344<433 B、433<344<255 C、255<433<344 D、344<433<255二、填空题
-
11. 计算:(﹣x3y)2= .12. 计算:( ab2 )2·a 2b3 =13. 若(2an)3=40,则a6n= .14. 若43×83=2x , 则x=。15. 若x+2y-3=0,则2x·4y的值为_。16. 已知M是单项式,且 ,则M=17. 若a=233 , b=322 , 则a、b的大小关系是a b.(填“>”、“<”或“=”)18. 若an=2,am=5,则am+n=;若2m=3,23n=5,则8m+2n= .
三、解答题
-
19. 计算:
(1)、 ;
(2)、(-3x2y)2·(-xyz)·xz2;(3)、(-4ab3)(-ab)-(ab2)2.20. 已知10x=a,5x=b,求:(1)、50x的值;(2)、2x的值;(3)、20x的值.(结果用含a、b的代数式表示)21.(1)、已知a= ,mn=2,求a2·(am)n的值;(2)、若 ,求 的值.22.(1)、已知m+4n-3=0,求2m·16n的值.(2)、已知n为正整数,且x2n=4,求(x3n)2-2(x2)2n的值.23. 已知 , ,试说明P=Q.24. 解答下列问题(1)、已知2x=3,2y=5,求2x+y的值;(2)、已知3m=4,3n=2,求 的值;(3)、若 ,求 的值.25. 阅读下列材料:若a3=2,b5=3,则a,b的大小关系是ab(填“<”或“>”).
解:因为a15=(a3)5=25=32,b15=(b5)3=33=27,32>27,所以a15>b15 ,
所以a>b.
解答下列问题:
①上述求解过程中,逆用了哪一条幂的运算性质
A.同底数幂的乘法 B.同底数幂的除法 C.幂的乘方 D.积的乘方
②已知x7=2,y9=3,试比较x与y的大小.
26. 规定两数a、b之间的一种运算,记作(a,b):如果 ,那么(a,b)=c.例如:因为 ,所以(2,8)=3.
(1)、根据上述规定,填空:(5,125)= , (-2,4)= , (-2,-8)=;
(2)、小明在研究这种运算时发现一个现象: ,他给出了如下的证明:设 ,则 ,即
∴ ,即 ,
∴ .
请你尝试运用上述这种方法说明下面这个等式成立的理由.
(4,5)+(4,6)=(4,30)