蒙古奈曼旗教科体局义务教育联盟初中二区2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-01-14 类型:月考试卷
一、单选题
-
1. 下列方程中,一定是一元二次方程的是( )A、2x2- +1=0 B、(x+2)(2x-1)=2x2 C、5x2-1=0 D、ax2+bx+c=02. 方程 的二次项系数、一次项系数及常数项的和是( )A、 B、 C、 D、3. 如果-1是方程x2-3x+k=0的一个根,则常数k的值为( )A、4 B、2 C、-4 D、-24. 一元二次方程x2+2x+2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、无实数根5. 用配方法解方程 变形后为( )A、 B、 C、 D、6. 某超市1月份营业额为90万元,1月、2月、3月总营业额为144万元,设平均每月营业额增长率为x , 则下面所列方程正确的是( )A、90(1+x)2=144 B、90(1-x)2=144 C、90(1+2x)=144 D、90(1+x)+90(1+x)2=144-907. 一元二次方程(x-5)2= x -5的解是( )A、x=5 B、x=6 C、x=0 D、x1=5,x2=68. 关于 的方程 有实数根,则 满足( )A、 B、 且 C、 且 D、9. 若关于 的一元二次方程 有两个不相等的实数根,则一次函数
的图象可能是:( )
A、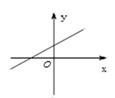 B、
B、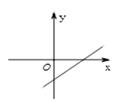 C、
C、 D、
D、
二、填空题
-
10. 关于x的方程 当m时,是一元一次方程;当m时,是一元二次方程.11. 写出一个解为1和2的一元二次方程:.12. 参加一次商品交易会的每两家公司之间都签订了一份合同,所有公司共签订了45份合同,设共有x家公司参加商品交易会,则可列出方程为:.13. 一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是57,每个支干长出个小分支.14. 一个等腰三角形的底边长是6,腰长是一元二次方程x2-7x+12=0的一个根,则此三角形的周长是 .15. 若m是方程2x2-3x-1=0的一个根,则6m2-9m+2015的值为 .16. 如图是一张长9cm、宽5cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是12cm2的一个无盖长方体纸盒,设剪去的正方形边长为xcm,则可列出关于x的方程为 .

三、解答题
-
17. 解方程:(1)、 ;(配方法)(2)、 .(公式法)18. 关于x的一元二次方程 有实数根,(1)、求m的取值范围;(2)、若方程有一个根为 ,求m的值和另一根.19. 奈曼旗某中学要组织一次篮球赛,赛制为双循环形式(每两队之间赛两场),计划安排12场比赛,应邀请多少支球队参加比赛?20. 在实数范围内定义一种新运算“△”,其规则为:a△b=a2-b2 , 根据这个规则:(1)、求4△3的值;(2)、求(x+2)△5=0中x的值.21.
如图,某农场有一块长40m , 宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2 , 求小路的宽
 22. 安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量 (千克)与每千克降价 (元) 之间满足一次函数关系,其图象如图所示:
22. 安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量 (千克)与每千克降价 (元) 之间满足一次函数关系,其图象如图所示: (1)、求 与 之间的函数关系式;(2)、商贸公司要想获利2090元,则这种干果每千克应降价多少元?23. 如图, 中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P同时停止运动.
(1)、求 与 之间的函数关系式;(2)、商贸公司要想获利2090元,则这种干果每千克应降价多少元?23. 如图, 中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P同时停止运动. (1)、运动几秒时 的面积为5cm2?(2)、运动几秒时 中PQ=6 cm?(3)、 的面积能否等于10cm2?若能,求出运动时间,若不能,说明理由.
(1)、运动几秒时 的面积为5cm2?(2)、运动几秒时 中PQ=6 cm?(3)、 的面积能否等于10cm2?若能,求出运动时间,若不能,说明理由.