河北省石家庄市石家庄外国语教育集团2020-2021学年九年级上学期数学第二次月考试卷

试卷更新日期：2021-01-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 二次函数 $y = {(x - 1)}^{2} - 2$ 的对称轴是（）

A、 $x = - 2$ B、 $x = - 1$ C、 $x = 2$ D、 $x = 1$

查看试题解析
2. 如图， $△ A B C$ 的顶点都是正方形网格中的格点，则 $\tan ∠ A B C$ 等于（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{\sqrt{10}}{10}$

查看试题解析
3. 如图，小明在一条东西走向公路的O处，测得图书馆A在他的北偏东60°方向，且与他相距200m，则图书馆A到公路的距离AB为（）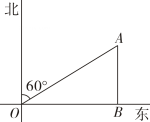

A、100m B、100 $\sqrt{2}$ m C、100 $\sqrt{3}$ m D、 $\frac{200 \sqrt{3}}{3}$ m

查看试题解析
4. 如图，直线l₁∥l₂∥l₃ ，直线AC和DF被l₁ ， l₂ ， l₃所截，AB＝5，BC＝6，EF＝4，则DE的长为（）

A、2 B、3 C、 $\frac{10}{3}$ D、4

查看试题解析
5. 在平面直角坐标系中，二次函数y=x²+2的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
6. 如图， $△ A B C$ 与 $△ A D E$ 成位似图形，位似中心为点 $A$ ，若 $A D ： A B = 1 ： 3$ ，则 $△ A D E$ 与 $△ A B C$ 面积之比为（）

A、 $1 ： 2$ B、 $1 ： 3$ C、 $1 ： 9$ D、 $1 ： 16$

查看试题解析
7. 如图，在 $⊙ O$ 中，点 $A$ ， $B$ ， $C$ 在 $⊙ O$ 上，且 $∠ A C B = 100^{°}$ ，则 $∠ α =$ （）

A、 $80^{°}$ B、 $100^{°}$ C、 $120^{°}$ D、 $160^{°}$

查看试题解析
8. 已知点 $A (1, y_{1}), B (2, y_{2})$ 在反比例函数 $y = - \frac{3}{x}$ 的图象上，则下列结论正确的是（）

A、 $y_{1} < y_{2} < 0$ B、 $0 < y_{1} < y_{2}$ C、 $y_{2} < y_{1} < 0$ D、 $0 < y_{2} < y_{1}$

查看试题解析
9. 如图，在 $⊙ O$ 中，弦AB垂直平分半径OC，OC=2，则弦AB的长为（）

A、 $2 \sqrt{3}$ B、 $\sqrt{3}$ C、 $2 \sqrt{2}$ D、 $\sqrt{2}$

查看试题解析
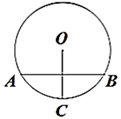10. 扬帆中学有一块长 $30 m$ ，宽 $20 m$ 的矩形空地，计划在这块空地上划出四分之一的区域种花，小禹同学设计方案如图所示，求花带的宽度．设花带的宽度为 $x m$ ，则可列方程为（）

A、 $(30 - x) (20 - x) = \frac{3}{4} \times 20 \times 30$ B、 $(30 - 2 x) (20 - x) = \frac{1}{4} \times 20 \times 30$ C、 $30 x + 2 \times 20 x = \frac{1}{4} \times 20 \times 30$ D、 $(30 - 2 x) (20 - x) = \frac{3}{4} \times 20 \times 30$

查看试题解析
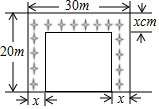11. 已知圆锥的底面半径为 $6 cm$ ，母线长为 $10 cm$ ，则这个圆锥的侧面积是（）

A、 $60 π {cm}^{2}$ B、 $96 π {cm}^{2}$ C、 $120 π {cm}^{2}$ D、 $168 π {cm}^{2}$

查看试题解析
12. 一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮，球沿一条抛物线运动，当球运动的水平距离为2.5m时，达到最大高度3.5m，然后准确落入篮框内．已知篮圈中心距离地面高度为3.05m，在如图所示的平面直角坐标系中，下列说法正确的是（）

A、此抛物线的解析式是y=- $\frac{1}{5}$ x²+3.5 B、篮圈中心的坐标是（4，3.05） C、此抛物线的顶点坐标是（3.5，0） D、篮球出手时离地面的高度是2m

查看试题解析
13. 如图，在平面直角坐标系中有一矩形 $A B C D$ 灰色区域，其中 $A B = 1 ， A D = 4$ ，点 $C (2 ， 1)$ ，有一动态扫描线为双曲线 $y = \frac{k}{x} (x > 0)$ ，当扫描线遇到灰色区域时，区域便由灰变亮，则下列能够使灰色区域变亮的 $k$ 的值不可能是（）

A、 $k = 1$ B、 $k = 2.2$ C、 $k = \sqrt{10}$ D、 $k = 4$

查看试题解析
14. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象上部分点的坐标 $(x, y)$ 对应值列表如下：

x

…

0

1

2

3

…

y

…

-2

-3

-2

…

则下列说法错误的是（）

A、抛物线开口向上． B、抛物线的对称轴为直线 $x = 1$ C、当 $x > 2$ 时， $y$ 随 $x$ 的增大而增大 D、方程 $a x^{2} + b x + c = 0$ 有一个根小于 $- 1$

查看试题解析
15. 如图，四边形 $A B C D$ 中， $A B = A D ， B C = D C ， ∠ A = 90^{°} ， ∠ C = 60^{°}$ ．若 $A B = 5 \sqrt{6}$ ．则 $△ A B D$ 外心与 $△ B C D$ 外心的距离是（）

A、5 B、 $5 \sqrt{3}$ C、 $\frac{10}{3}$ D、 $\frac{10}{3} \sqrt{3}$

查看试题解析
16. 已知锐角 $∠ A O B$ ，如图，

⑴在射线 $O A$ 上取一点 $C$ ，以点 $O$ 为圆心， $O C$ 长为半径作 $\overset{⌢}{P Q}$ ，交射线 $O B$ 于点 $D$ ，连接 $C D$ ；

⑵分别以点 $C$ ， $D$ 为圆心， $C D$ 长为半径作弧，交 $\overset{⌢}{P Q}$ 于点 $M$ ， $N$ ；

⑶连接 $O M ， M N ， D N$ ．

根据以上作图过程及所作图形，下列结论中正确的个数为的（）

① $∠ C O M = ∠ C O D$ ；②若 $O M = M N$ ．则 $∠ A O B = 20^{°}$ ；

③ $∠ M O D = ∠ M N D$ ；④ $M N / / C D$ ；⑤ $M N = 3 C D$ ；

A、1个 B、2个 C、3 D、4个

查看试题解析

二、填空题

17. 若m是方程 $x^{2} - 3 x - 1 = 0$ 的根，则 $1 - m^{2} + 3 m$ 的值为．

查看试题解析
18. 如下图是在量角器的圆心 $O$ 处下挂一铅锤，制作了一个简易测角仪，右图是借助这个测角仪测量大楼高度的示意图．当量角器的0度线 $A B$ 对准楼顶时，铅垂线对应的读数是 $50^{°}$ ，则此时观察楼顶的仰角度数是．

查看试题解析
19. 已知正方形 $A B C D$ 的边长为6， $E$ 在射线 $C B$ 上运动，且点 $E$ 与点 $C$ 不重合， $D E$ 的中点 $G$ ， $E G$ 绕 $E$ 顺时针旋转 $90^{°}$ 得 $E F$ ，

则：

(1)、当 $E$ 与点 $B$ 重合时（如图2），求点 $F$ 到直线 $B C$ 距离是．

(2)、若点 $F$ 落在正方形边所在的直线上时， $C E$ 的长为．

查看试题解析

三、解答题

20. 根据要求回答：

(1)、计算： $2 \sin 30^{°} - \sqrt{12} + {(- 2020)}^{0}$ ．

(2)、已知关于 $x$ 的方程 $x^{2} - 4 x + a = 0$ ，若此方程有两个相等的实数根，求 $a$ 的值：并求出该方程的解。

查看试题解析
21. 如图， $△ A B C$ 内接于 $⊙ O$ ， $∠ B A C = 120^{°} ， A B = A C = 2$ ，

(1)、求 $∠ C$ 的度数；

(2)、求 $⊙ O$ 的直径．

查看试题解析
22. 想了解某次数学测验的成绩情况，抽样调查了九年级（7）班的成绩，分别记作60分、70分、80分、90分、100分，并将统计结果绘制成不完整的统计图（如图）．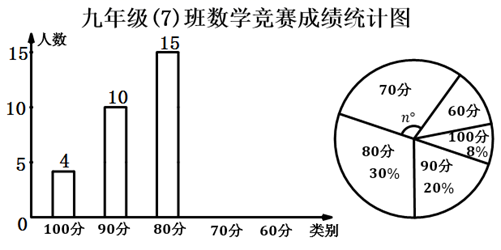

(1)、样本容量为，成绩的中位数为；

(2)、若成绩为60分的人数为6人，则 $n$ = ．

(3)、若全校有1500人，估计全校90分及以上的同学大约多少人？

查看试题解析
23. 若商场为方便消费者购物，准备将原来的阶梯式自动扶梯改造成斜坡式动扶梯，如图所示，已知原阶梯式自动扶梯 $A B$ 长为10m，扶梯 $A B$ 的坡度 $i$ 为 $1 ： \sqrt{3}$ ．改造后的斜坡式动扶梯的坡角 $∠ A C B$ 为 $15^{°}$

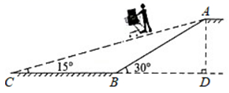(1)、请你求出 $A D$ 的长度；

(2)、请你计算改造后的斜坡式自动扶梯 $A C$ 的长度．（结果精确到0.1m．参考数据： $\sin 15^{°} \approx 0.26 ， \cos 15^{°} \approx 0.97 ， \tan 15^{°} \approx 0.27$ ）

查看试题解析
24. 已知：抛物线 $y = - x^{2} + 2 x + m$ ．

(1)、若抛物线过点 $A (3 ， 0)$ ，与 $y$ 轴交于点 $B$ ，与 $x$ 轴的另一个交点是点 $C$ ．
①求这个抛物线的解析式，并求出点 $B$ ， $C$ 的坐标；

②若该抛物线有一点 $D (x ， y)$ ，且点 $D$ 与点 $B$ 不重合，若 $S_{△ A B C} = S_{△ A C D}$ ，求点 $D$ 的坐标．

(2)、若 $M (- 1 ， 3)$ ， $N (4 ， 3)$ ，抛物线 $y = - x^{2} + 2 x + m$ 与线段 $M N$ 有两个不同交点，则 $m$ 的取值范围是．

查看试题解析
25. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90^{°}$ $A C = 6 ， B C = 8$ ，动点 $P$ 沿线段 $C B$ 从点 $C$ 向点 $B$ 运动，当点 $P$ 与点 $B$ 重合时，停止运动，以点 $P$ 为圆心， $P C$ 为半径作 $⊙ P$ ，点 $M$ 在 $⊙ P$ 上且在 $△ A B C$ 外， $∠ C P M = 90^{°}$ ．

(1)、当 $C P = 2 \sqrt{3}$ 时 $A P =$ ，点 $A$ 到 $⊙ P$ 的最远距离为；

(2)、 $⊙ P$ 与 $A B$ 相切于点 $D$ 时（如图2），求 $P C$ 的长？并求出此时劣弧 $\overset{⌢}{C D}$ 长度？（参考数据： $\sin 37^{°} = \frac{3}{5} ， \tan 37^{°} = \frac{3}{4}$ ）

(3)、直接写出点 $M$ 的运动路径长为， $B M$ 的最短距离为．

查看试题解析
26. 某公司为了宣传一种新产品，在某地先后举行40场产品促销会，已知该产品每台成本为10万元，设第 $x$ 场产品的销售量为 $y$ （台），在销售过程中获得以下信息：信息1：第一场销售产品49台，第二场销售产品48台，且销售量 $y$ 与 $x$ 是一次函数关系；信息2：产品的每场销售单价 $p$ （万元）由基本价和浮动价两部分组成，其中基本价保持不变，第1场至第29场浮动价与销售场次 $x$ 成正比，第30场至第40场浮动价与销售场次 $x$ 成反比，经过统计，得到如下数据：

$x$ （场）

3

10

35

$p$ （万元）

10.6

12

13

(1)、直接写出 $y$ 与 $x$ 之间满足的函数关系式；

(2)、求 $p$ 与 $x$ 函数关系式，并写出自变量的取值范围；

(3)、在这40场产品促销会中，哪一场获得的利润最大，最大利润是多少？

查看试题解析

x	…	0	1	2	3	…
y	…	-2	-3	-2		…

$x$ （场）	3	10	35
$p$ （万元）	10.6	12	13