河北省沧州市14中2020-2021学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-01-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列关于 $x$ 的方程：① $a x^{2} + b x + c = 0$ ；② $x^{2} + \frac{1}{x^{2}} - 3 = 0$ ；③ $x^{2} - 4 + x^{5} = 0$ ；④ $3 x = x^{2}$ ．其中是一元二次方程的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 一元二次方程 ${(3 x -1)}^{2} = 5 x$ 化简成一般式后，二次项系数为9，其一次项系数为（）

A、1 B、-1 C、-11 D、11

查看试题解析
3. 抛物线 $y = x^{2} - 6 x + 4$ 的顶点坐标是（）

A、 $(3 ， 5)$ B、 $(- 3 ， 5)$ C、 $(3 ， - 5)$ D、 $(- 3 ， - 5)$

查看试题解析
4. 下列图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 风力发电机可以在风力作用下发电．如图的转子叶片图案绕中心旋转n°后能与原来的图案重合，那么n的值可能是（）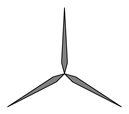

A、45 B、60 C、90 D、120

查看试题解析
6. 把函数 $y = 3 x^{2}$ 的图像向下平移2个单位长度，所得到的新函数的解析式是（）

A、 $y = 3 {(x - 2)}^{2}$ B、 $y = 3 x^{2} + 2$ C、 $y = 3 x^{2} - 2$ D、 $y = 3 {(x + 2)}^{2}$

查看试题解析
7. 关于二次函数y＝2(x－2)²＋5，下列说法错误的是（）

A、图象与y轴的交点坐标为（0，13） B、图象的对称轴在y轴的右侧 C、当x>0时，y的值随x值的增大而增大 D、当x=2时，函数有最小值为5

查看试题解析
8. $a$ 是方程 $x^{2} + x - 1 = 0$ 的一个根，则代数式 $- 2 a^{2} - 2 a + 2020$ 的值是（）

A、2018 B、2019 C、2020 D、2021

查看试题解析
9. 正方形的边长为3，边长增加x，面积增加y，则y关于x的函数解析式为（）

A、 $y = {(x + 3)}^{2}$ B、 $y = x^{2} + 9$ C、 $y = x^{2} + 6 x$ D、 $y = 3 x^{2} + 12 x$

查看试题解析
10. 如图，在长 $70 m$ ，宽 $40 m$ 的矩形花园中，欲修宽度相等的观赏路（阴影部分），要使观赏路面积占总面积的 $\frac{1}{7}$ ，则路宽 $x m$ 应满足的方程是（）.

A、 $(40 - x) (70 - x) = 400$ B、 $(40 - 2 x) (70 - 3 x) = 400$ C、 $(40 - x) (70 - x) = 2400$ D、 $(40 - 2 x) (70 - 3 x) = 2400$

查看试题解析
11. 某商品价格从2017年底到2018年底下降19%，从2018年底到2019年底下降36%，那么此商品价格从2017年底到2019年底平均下降百分率为：（）

A、30% B、28% C、25.5% D、20%

查看试题解析
12. 已知抛物线 $y = a x {}^{2}+ b x + c$ 与x轴的两个交点坐标是（-2，0），（5，0），则一元二次方程 $a x^{2} + b x + c = 0$ 的两个解是（）

A、 $x_{1} = - 2, x_{2} = 5$ B、 $x_{1} = 2, x_{2} = - 5$ C、 $x_{1} = - 2, x_{2} = - 5$ D、 $x_{1} = 2, x_{2} = 5$

查看试题解析
13. 从地面竖直向上抛出一小球，小球的高度 h （单位： m ）与小球运动时间 $t$ （单位： s ）之间的函数关系如图所示．下列结论：
①小球在空中经过的路程是 40m ；②小球运动的时间为 6s ；③小球抛出3秒时，速度为0；

④当 $t = 1.5 s$ 时，小球的高度 $h = 30 m$ ．其中正确的是（）

A、①④ B、①② C、②③④ D、②④

查看试题解析
14. 根据表中的自变量x与函数y的对应值，可判断此函数解析式为（）

A、 $y = x$ B、 $y = - \frac{1}{x}$ C、 $y = \frac{3}{4} {(x - 1)}^{2} + 2$ D、 $y = - \frac{3}{4} {(x - 1)}^{2} + 2$

查看试题解析
15. 抛物线y=ax²+bx+c的对称轴为直线x=﹣1，部分图象如图所示，下列判断中：
①abc＞0；②b²﹣4ac＞0；③9a﹣3b+c=0；④若点（﹣0.5，y₁），（﹣2，y₂）均在抛物线上，则y₁＞y₂；⑤5a﹣2b+c＜0．其中正确的个数有（）

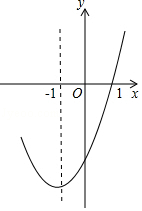A、2 B、3 C、4 D、5

查看试题解析
16. 已知点P（m，n）在抛物线 $y = x (x - 2)$ 上，针对n的不同取值，所找点P的个数，三人的说法如下：甲：若n=-2，则点P的个数为0．乙：若n=-1，则点P的个数为1．丙：若n=4，则点P的个数为0．下列判断正确的是（）

A、乙错，丙对 B、甲和乙都错 C、乙对，丙错 D、甲错，丙对

查看试题解析

二、填空题

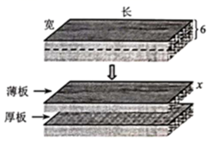
17. 点M(1，a)和点N（b，-2)关于原点对称，则（a+b）²⁰²⁰= ．

查看试题解析
18. 用公式法解一元二次方程，得x= $\frac{- 5 \pm \sqrt{5^{2} - 4 \times 3 \times 1}}{2 \times 3}$ ，则该一元二次方程是。

查看试题解析
19. 抛物线 $y = x^{2} - 2 x - 3$ 与 $x$ 轴有两个交点，则原点左侧交点坐标为.

查看试题解析
20. 用承重指数W衡量水平放置得长方体木板的最大称重量．实验发现：木板承重指数W与木板厚度x（厘米）的平方成正比，当x=3时，W=3．选一块厚度为6厘米的木板，把它分割成与原来同长同宽但薄厚不同的两块板（不计分割损耗）．设薄板的厚度为x（厘米），Q=W_厚-W_薄，当x=时，Q=3W_薄．

查看试题解析

三、解答题

21. 解方程：

(1)、 ${(x - 2)}^{2} = 2$ ；

(2)、 $x^{2} - 2 x - 3 = 0$ ；

(3)、 $2 x^{2} + x + 1 = 0$

查看试题解析
22. 对于实数a，b，定义新运算“*”：a*b＝ ${\begin{array}{l} a^{2} - a b (a ⩾ b) \\ a b - b^{2} (a < b) \end{array}$ ，例如：4*2，因为4＞2，所以4*2＝4²﹣4×2＝8.

(1)、求（﹣7）*（﹣2）的值；

(2)、若x₁ ， x₂是一元次方程x²﹣5x﹣6＝0的两个根，求x₁*x₂的值.

查看试题解析
23. 某商店购进一批单价为8元的商品，如果每件10元出售，那么每天可销售100件，经调查发现，这种商品的销售单价每提高1元，其销售量相应减少10件．

(1)、求销售量y件与销售单价x（元）之间的解析式．（不用标出自变量的取值范围）

(2)、当销售单价定为多少时？才能使每天所获销售利润最大？最大利润是多少？

查看试题解析
24. 已知抛物线经过A(1，0)，B(5，0)，C(0，4)，Q四个点，且点Q在x轴下方．

(1)、求抛物线的解析式和对称轴；

(2)、P是抛物线对称轴上的一点，直接写出满足PA+PC的值为最小的点P坐标；

(3)、点Q是否能使得△ABQ的面积和△ABC的面积相等？若能，请直接写出此时的点Q的坐标；若不能，请说明理由．

查看试题解析
25. 已知△ABC中，∠ABC=90°，∠C=30°，AB=1．若把△ABC绕点B顺时针旋转得到△EBD，

(1)、如图1，当点E落在AC边上时，求旋转角度大小．

(2)、如图2，当点E落在直线CD上时，求点C和点D之间的距离．

查看试题解析