山西省朔州市朔城区2020-2021学年八年级上学期数学第三次月考试卷
试卷更新日期:2021-01-14 类型:月考试卷
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,点B、F、C、E在一条直线上, , ,要使 ≌ ,需要添加下列选项中的一个条件是( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,点B、F、C、E在一条直线上, , ,要使 ≌ ,需要添加下列选项中的一个条件是( )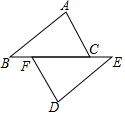 A、 B、 C、 D、4. 已知△ABC中,∠A与∠C的度数比为5:7,且∠B比∠A大10°,那么∠B为( )A、40° B、50° C、60° D、70°5. 在边长为 的正方形中挖掉一个边长为 的小正方形,把余下的部分剪拼成一个长方形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,这个等式是( )
A、 B、 C、 D、4. 已知△ABC中,∠A与∠C的度数比为5:7,且∠B比∠A大10°,那么∠B为( )A、40° B、50° C、60° D、70°5. 在边长为 的正方形中挖掉一个边长为 的小正方形,把余下的部分剪拼成一个长方形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,这个等式是( ) A、 B、 C、 D、6. 如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB=( )
A、 B、 C、 D、6. 如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB=( ) A、30° B、45° C、60° D、90°7. 下列从左边到右边的变形,是因式分解的是( )A、 B、 C、 D、8. 如图,在△ABC中,∠C=90°,AC=2,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是( )
A、30° B、45° C、60° D、90°7. 下列从左边到右边的变形,是因式分解的是( )A、 B、 C、 D、8. 如图,在△ABC中,∠C=90°,AC=2,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是( )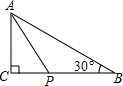 A、2 B、3 C、4 D、59. 已知 , ,则 的值是( )A、70 B、76 C、80 D、8410. 在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,在 轴上有一点 使 的值最小,则点 的坐标为( )A、 B、 C、 D、
A、2 B、3 C、4 D、59. 已知 , ,则 的值是( )A、70 B、76 C、80 D、8410. 在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,在 轴上有一点 使 的值最小,则点 的坐标为( )A、 B、 C、 D、二、填空题
-
11. 计算: 的结果为 .12. 如图,在 中, , , 的垂直平分线交 于点 ,交 于点 ,则 的度数是 .
 13. 因式分解: .14. 若 是一个完全平方式,则 .15. 如图, 平分 交 于点 , 于点 ,若 , , ,则 的长为 .
13. 因式分解: .14. 若 是一个完全平方式,则 .15. 如图, 平分 交 于点 , 于点 ,若 , , ,则 的长为 .
三、解答题
-
16.(1)、如图,在平面直角坐标系中,作 关于 轴对称的 .
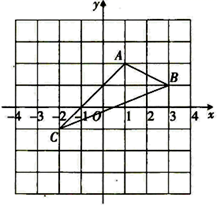 (2)、计算: .17. 如图,在 中, 为高, 为 的平分线,若 , ,求 的度数.
(2)、计算: .17. 如图,在 中, 为高, 为 的平分线,若 , ,求 的度数.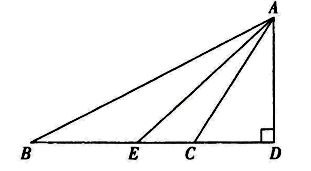 18. 已知 ,求代数式 的值.19. 如图,∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
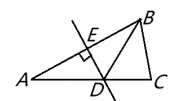
18. 已知 ,求代数式 的值.19. 如图,∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.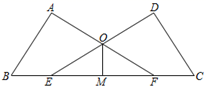 (1)、求证:AF=DE;(2)、若OM平分∠EOF,求证:OM⊥EF.20.(1)、已知 , ,求 的值.(2)、已知 , ,求 的值.21. 如图, 是边长为1的等边三角形, , ,点 , 分别在 , 上,且 ,求 的周长.
(1)、求证:AF=DE;(2)、若OM平分∠EOF,求证:OM⊥EF.20.(1)、已知 , ,求 的值.(2)、已知 , ,求 的值.21. 如图, 是边长为1的等边三角形, , ,点 , 分别在 , 上,且 ,求 的周长.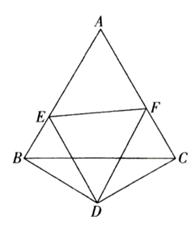 22. 综合与实践
22. 综合与实践下面是某同学对多项式 进行因式分解的过程:
解:设 ,
原式 (第一步)
(第二步)
(第三步)
(第四步).
回答下列问题:
(1)、该同学第二步到第三步运用了________.A、提取公因式 B、平方差公式 C、两数差的完全平方公式 D、两数和的完全平方公式(2)、该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”),若不彻底,则该因式分解的最终结果为 .(3)、请你模仿上述方法,对多项式 进行因式分解.23. 综合与探究(阅读理解)在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为 的正方形,乙种纸片是边长为 的正方形,丙种纸片是长为 ,宽为 的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
 (1)、①观察图2,用两种不同方式表示阴影部分的面积可得到一个等式:
(1)、①观察图2,用两种不同方式表示阴影部分的面积可得到一个等式:②利用①中的等式解决问题:若 , ,则 的值为 .
(2)、(拓展探究)若 满足 ,求 的值.我们可以作如下解答:设 , ,
则 , ,
所以 .
①若 ,则 .
②若 ,则 .
(3)、(实际运用)如图3,将正方形 叠放在正方形 上,重叠部分 是一个长方形, , .沿着 、 所在直线将正方形 分割成四个部分,若四边形 和四边形 恰好为正方形,且它们的面积之和为400,求长方形 的面积.