浙江省宁波市北仑区七校精准教学联盟2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-01-14 类型:期中考试
一、单选题
-
1. 下列四个图案中,不是轴对称图案的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法正确的是( )A、一个命题一定有逆命题 B、一个定理一定有逆定理 C、真命题的逆命题一定是真命题 D、假命题的逆命题一定是假命题3. 长度分别为3,8,x的三条线段能组成一个三角形,x的值可以是( )A、4 B、5 C、6 D、114. 若 ,则下列各式正确的是( )A、 B、 C、 D、5. 如图所示,亮亮课本上的三角形被墨迹涂抹了一部分,但他根据所学知识很快画出了一个完全一样的三角形,那么这两个三角形完全一样的依据是( )
2. 下列说法正确的是( )A、一个命题一定有逆命题 B、一个定理一定有逆定理 C、真命题的逆命题一定是真命题 D、假命题的逆命题一定是假命题3. 长度分别为3,8,x的三条线段能组成一个三角形,x的值可以是( )A、4 B、5 C、6 D、114. 若 ,则下列各式正确的是( )A、 B、 C、 D、5. 如图所示,亮亮课本上的三角形被墨迹涂抹了一部分,但他根据所学知识很快画出了一个完全一样的三角形,那么这两个三角形完全一样的依据是( ) A、SSS B、SAS C、AAS D、ASA6. 如图,已知 ,那么添加下列一个条件后,仍无法判定 的是( )
A、SSS B、SAS C、AAS D、ASA6. 如图,已知 ,那么添加下列一个条件后,仍无法判定 的是( )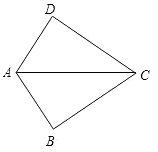 A、 B、 C、 D、7. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、7. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知 的三条边长分别为 , , ,三个角分别为 , , ,则不能证明 为直角三角形的是( )A、 B、 C、 D、9. 已知:如图, 是 内部的一条射线, 是射线 上任意一点, , ,垂足分别为 , .有下列条件:① ;② ;③ ;④ .其中,能判定 是 的平分线的有( )
8. 已知 的三条边长分别为 , , ,三个角分别为 , , ,则不能证明 为直角三角形的是( )A、 B、 C、 D、9. 已知:如图, 是 内部的一条射线, 是射线 上任意一点, , ,垂足分别为 , .有下列条件:① ;② ;③ ;④ .其中,能判定 是 的平分线的有( ) A、1个 B、2个 C、3个 D、4个10. 如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是( )
A、1个 B、2个 C、3个 D、4个10. 如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是( )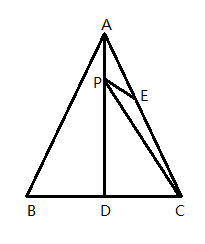 A、30° B、45° C、60° D、90°
A、30° B、45° C、60° D、90°二、填空题
-
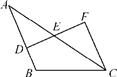
11. 在△ABC中,已知∠A=60°,∠B=80°,则∠C=.12. 命题“如果a>0,那么a2>0”的逆命题为.13. “ 的2倍与 的差小于 ”用不等式表示.14. 若一个等腰三角形的两边长分别为6和11,则这个三角形的周长为.15. 如图,已知AB∥CF,点E为DF的中点,若AB=9 cm,CF=5 cm,则BD=cm.
 16. 已知不等式mx+n>0的解集为x<2,则 的值是.17. 如图,锐角 和锐角 中, , 分别是 , 上的高,且 , .要使 ,则应补充的条件是(填写一个即可).
16. 已知不等式mx+n>0的解集为x<2,则 的值是.17. 如图,锐角 和锐角 中, , 分别是 , 上的高,且 , .要使 ,则应补充的条件是(填写一个即可). 18. 如图,长方形纸片 , , ,点 在 边上,将 沿 折叠,点 落在 处, , 分别交 于点 , ,且 ,则 长为.
18. 如图,长方形纸片 , , ,点 在 边上,将 沿 折叠,点 落在 处, , 分别交 于点 , ,且 ,则 长为.
三、解答题
-
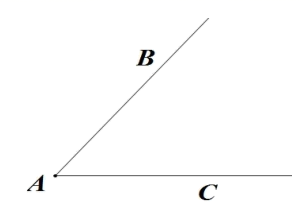
19. 尺规作图:已知: ,求作 的平分线.
 20. 在如图所示的网格中,每个小正方形的边长均为1个单位.
20. 在如图所示的网格中,每个小正方形的边长均为1个单位. (1)、请你在图1中画一个以格点为顶点,面积为4个平方单位的等腰三角形;(2)、请你在图2中画一个以格点为顶点,一条直角边长为 个单位的直角三角形.21. 如图,点 、 在线段 上, , , ,试说明 .
(1)、请你在图1中画一个以格点为顶点,面积为4个平方单位的等腰三角形;(2)、请你在图2中画一个以格点为顶点,一条直角边长为 个单位的直角三角形.21. 如图,点 、 在线段 上, , , ,试说明 . 22. 解一元一次不等式组 并写出它的整数解.23. 如图,在 中,已知点 在线段 的反向延长线上,过 的中点 作线段 交 的平分线于 ,交 于 ,且 .
22. 解一元一次不等式组 并写出它的整数解.23. 如图,在 中,已知点 在线段 的反向延长线上,过 的中点 作线段 交 的平分线于 ,交 于 ,且 . (1)、求证: 是等腰三角形:(2)、若 , ,求 的长.24. 某商家预测“华为P30”手机能畅销,就用1600元购进一批该型号手机壳,面市后果然供不应求,又购进6000元的同种型号手机壳,第二批所购买手机壳的数量是第一批的3倍,但进货单价比第一批贵了2元.(1)、第一批手机壳的进货单价是多少元?(2)、若两次购进于机壳按同一价格销售,全部传完后,为使得获利不少于2000元,那么销售单价至少为多少?
(1)、求证: 是等腰三角形:(2)、若 , ,求 的长.24. 某商家预测“华为P30”手机能畅销,就用1600元购进一批该型号手机壳,面市后果然供不应求,又购进6000元的同种型号手机壳,第二批所购买手机壳的数量是第一批的3倍,但进货单价比第一批贵了2元.(1)、第一批手机壳的进货单价是多少元?(2)、若两次购进于机壳按同一价格销售,全部传完后,为使得获利不少于2000元,那么销售单价至少为多少?

