河北省临西县2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期:2021-01-14 类型:月考试卷
一、单选题
-
1. 下列四个选项中的图形与下面的图形全等的是( )
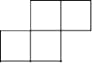 A、
A、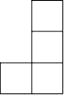 B、
B、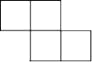 C、
C、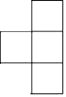 D、
D、 2. 赵师傅在做完门框后,为防止变形,按图中所示的方法在门上钉了两根斜拉的木条(图中的 两根木条),其中运用的几何原理是( )
2. 赵师傅在做完门框后,为防止变形,按图中所示的方法在门上钉了两根斜拉的木条(图中的 两根木条),其中运用的几何原理是( ) A、两点之间线段最短 B、三角形两边之和大于第三边 C、垂线段最短 D、三角形的稳定性3. 如图,CD是 的中线,若 ,则AD的长为( )
A、两点之间线段最短 B、三角形两边之和大于第三边 C、垂线段最短 D、三角形的稳定性3. 如图,CD是 的中线,若 ,则AD的长为( ) A、 B、 C、 D、4. 如图, ,且 ,则 的度数为( )
A、 B、 C、 D、4. 如图, ,且 ,则 的度数为( ) A、 B、 C、 D、5. 如图,六角螺母的横截面是正六边形,则 的度数为( )
A、 B、 C、 D、5. 如图,六角螺母的横截面是正六边形,则 的度数为( ) A、60° B、120° C、45° D、75°6. 如图,用三角板作 的边 上的高线,下列三角板的摆放位置正确的是( )A、
A、60° B、120° C、45° D、75°6. 如图,用三角板作 的边 上的高线,下列三角板的摆放位置正确的是( )A、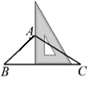 B、
B、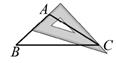 C、
C、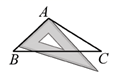 D、
D、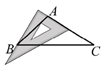 7. 将一副三角板按图中的方式叠放,则 的度数为( )
7. 将一副三角板按图中的方式叠放,则 的度数为( ) A、 B、 C、 D、8. 如图, , 四个点在同一直线上,若 ,则 的长是 ( )
A、 B、 C、 D、8. 如图, , 四个点在同一直线上,若 ,则 的长是 ( ) A、2 B、3 C、5 D、79. 在下列条件中:
A、2 B、3 C、5 D、79. 在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=2∠B=3∠C,④ 中,能确定△ABC是直角三角形的条件有( )
A、1个 B、2个 C、3个 D、4个10. 若将长度分别为 的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),则该三角形的最长边的长为( )A、 B、 C、 D、11. 下面是投影屏上出示的解答题,需要回答横线上符号代表的内容.如图,直线 直线 ,在 中, ,顶点 在 上,顶点 在 上,且 平分 ,若 ,求 的度数.

解:∵ , ,
∴ _______①_______,
∵直线 直线 ,
∴_____②______ ,
∵ 平分 ,
∴ _____③_____= ,
∵直线 直线 ,
∴ ___④_____= ,
下列选项错误的是( )
A、①代表64° B、②代表 C、③代表 D、④代表12. 如图,在 中, , , ,那么 的度数为( ) A、64° B、54° C、44° D、36°13. 在 中, ,若 的平分线 交于点 ,则 的度数是( )A、 B、 C、 D、14. 在△ABC中, ,则△ABC是( )A、等腰直角三角形 B、锐角三角形 C、钝角三角形 D、直角三角形15. 对于题目:如图, 是 的角平分线, 于点 ,若 ,求 的度数.下面是打乱了的解题过程:①∵ ;② ;③∵ 平分 ,∴ ;④∵ , ,则下列排序正确的是( ).
A、64° B、54° C、44° D、36°13. 在 中, ,若 的平分线 交于点 ,则 的度数是( )A、 B、 C、 D、14. 在△ABC中, ,则△ABC是( )A、等腰直角三角形 B、锐角三角形 C、钝角三角形 D、直角三角形15. 对于题目:如图, 是 的角平分线, 于点 ,若 ,求 的度数.下面是打乱了的解题过程:①∵ ;② ;③∵ 平分 ,∴ ;④∵ , ,则下列排序正确的是( ). A、③④②① B、④②①③ C、③②④① D、③①④②16. 如图, 中, ,且 , ,则 的度数为( )
A、③④②① B、④②①③ C、③②④① D、③①④②16. 如图, 中, ,且 , ,则 的度数为( ) A、80° B、60° C、40° D、20°
A、80° B、60° C、40° D、20°二、填空题
-
17. 在 中,若 , ,则 的度数为 .18. 三角形的外角和等于度.
三、解答题
-
19. 一个机器人以 的速度在平地上按如下要求行走,
 (1)、该机器人从开始到停止所走过的路程形成的图形是;(2)、该机器人从开始到停止所需时间为 ;(3)、若机器人还差 就第 次回到点 处,则它所走过的路程为 .20.(1)、如图1, 的外角 为116°, ,求 的余角的度数.
(1)、该机器人从开始到停止所走过的路程形成的图形是;(2)、该机器人从开始到停止所需时间为 ;(3)、若机器人还差 就第 次回到点 处,则它所走过的路程为 .20.(1)、如图1, 的外角 为116°, ,求 的余角的度数.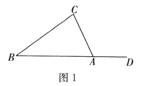 (2)、求图2中 的值.
(2)、求图2中 的值. 21. 如图, , , ,求 的度数.
21. 如图, , , ,求 的度数. 22. 如图,在 中, 平分 , 是 的反向延长线上一点, 于点 .若 , ,求 的度数.
22. 如图,在 中, 平分 , 是 的反向延长线上一点, 于点 .若 , ,求 的度数. 23. 已知 是 的三边长, ,设三角形的周长是 .(1)、尝试:分别写出 及 的取值范围.(2)、发现:当 为奇数时,求 的最大值和最小值.(3)、联想:若 是小于18的偶数,判断 的形状.24. 如图1,四边形 为一张长方形纸片.
23. 已知 是 的三边长, ,设三角形的周长是 .(1)、尝试:分别写出 及 的取值范围.(2)、发现:当 为奇数时,求 的最大值和最小值.(3)、联想:若 是小于18的偶数,判断 的形状.24. 如图1,四边形 为一张长方形纸片. (1)、如图2,将长方形纸片剪两刀,剪出三个角( ),则 °.(2)、如图3,将长方形纸片剪三刀,剪出四个角( ),则 °.(3)、如图4,将长方形纸片剪四刀,剪出五个角( ),则 °.(4)、根据前面探索出的规律,将本题按照上述剪法剪 刀,剪出 个角,那么这 个角的和是°.
(1)、如图2,将长方形纸片剪两刀,剪出三个角( ),则 °.(2)、如图3,将长方形纸片剪三刀,剪出四个角( ),则 °.(3)、如图4,将长方形纸片剪四刀,剪出五个角( ),则 °.(4)、根据前面探索出的规律,将本题按照上述剪法剪 刀,剪出 个角,那么这 个角的和是°.

