甘肃省白银市会宁县2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-01-14 类型：期中考试

进入出卷网下载

一、单选题

1. 以下列各组数为边长的三角形中，不能构成直角三角形的是（）

A、6，8，10 B、3，4，5 C、8，12，15 D、5，12，13

查看试题解析
2. 在直角 $△ A B C$ 中， $∠ A C B = 90 °$ ，如果 $A B = 4$ ， $A C = 3$ ，那么 $B C$ 的长是（）

A、2 B、5 C、 $\sqrt{7}$ D、5或 $\sqrt{7}$

查看试题解析
3. 下列各个数中，是无理数的是（）
$\sqrt{2}, \sqrt[3]{1000}, π, - 3.1416, \sqrt{9}, \frac{1}{3}, 0.030030003 \dots, 0.571 \overset{• •}{43}, \sqrt[3]{- 1}$

A、0个 B、1个 C、2个 D、3个

查看试题解析
4. $\sqrt{81}$ 的平方根是（）

A、±3 B、3 C、9 D、±9

查看试题解析
5. 若|a|=﹣a，则实数a在数轴上的对应点一定在（）

A、原点左侧 B、原点或原点左侧 C、原点右侧 D、原点或原点右侧

查看试题解析
6. 若点P在第二象限内，点P到x轴的距离是5，到y轴的距离是2，则点P的坐标为（）

A、(-5，2) B、（-5，-2） C、（-2，5） D、（-2，-5）

查看试题解析
7. 若函数 $y = (m + 1) x + m^{2} - 1$ 是关于 $x$ 的正比例函数，则 $m$ 的值（）

A、 $m = - 1$ B、 $m = 1$ C、 $m = \pm 1$ D、 $m = 2$

查看试题解析
8. 当1 $<$ a $<$ 2时，代数式 $\sqrt{{(a - 2)}^{2}}$ +|a﹣1|的值是（）

A、1 B、﹣1 C、2a﹣3 D、3﹣2a

查看试题解析
9.
如图，Rt△MBC中，∠MCB=90°，点M在数轴﹣1处，点C在数轴1处，MA=MB，BC=1，则数轴上点A对应的数是（）

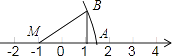A、 $\sqrt{5}$ +1 B、﹣ $\sqrt{5}$ +1 C、﹣ $\sqrt{5}$ ﹣l D、 $\sqrt{5}$ ﹣1

查看试题解析
10.
如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S₁ ， S₂ ，则S₁+S₂的值为（）

A、16 B、17 C、18 D、19

查看试题解析

二、填空题

11. 若 $Δ A B C$ 的三边 $a 、 b 、 c$ ,其中b=1，且 ${(a - 1)}^{2} + | c - \sqrt{2} | = 0$ ，则 $Δ A B C$ 的形状为.

查看试题解析
12. $- \sqrt{5}$ 的相反数为， $\sqrt{2} - 1$ 的绝对值是.

查看试题解析
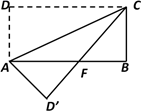
13. 如图，在矩形ABCD中，AB＝8，BC＝4，将矩形沿AC折叠，点D落在点D’处，则重叠部分△AFC的面积为．

查看试题解析
14. 在平面直角坐标系中，已知点P₁(a－1，6)和P₂(3，b－1)关于x轴对称，则(a＋b)²⁰²⁰的值为.

查看试题解析
15. 估算： $\sqrt{46} \approx$ （结果精确到1）.

查看试题解析
16. 已知实数a，b互为相反数，且|a+2b|＝1，b＜0，则b＝.

查看试题解析
17. 若 $x = \sqrt{2} - 3$ ，则代数式 $x^{2} + 6 x + 9$ 的值是.

查看试题解析
18. 已知实数 $\sqrt{3}$ 的整数部分是m，小数部分是n，则 $\frac{m}{n+3}$ ＝.

查看试题解析
19. $R t △ A B C$ 中，斜边BC＝2，则AB²+AC²+BC²的值为．

查看试题解析
20. 某下岗职工购进一批货物到集贸市场零售，已知卖出的货物质量x(千克)与售价y(元)的关系如表所示：

质量x(千克)

1

2

3

4

5

售价y(元)

2＋0.1

4＋0.2

6＋0.3

8＋0.4

10＋0.5

写出y关于x的函数关系式是.

查看试题解析

三、解答题

21. 计算

(1)、 ${(\sqrt{2})}^{2} - {(\frac{1}{3})}^{- 1} - {(\sqrt{3} + 1)}^{0}$ ；

(2)、 $(\sqrt{3} + 2) (\sqrt{3} - 2) + {(2 \sqrt{3} - 1)}^{2}$

(3)、 $\sqrt{20} - \sqrt{8} \div 2 \sqrt{\frac{1}{2}} + \sqrt{45}$ ；

(4)、 $(\frac{1}{3} \sqrt{27} + 2 \sqrt{\frac{2}{3}} - \sqrt{24}) \times 2 \sqrt{3}$

查看试题解析
22. 已知 $2 a - 1$ 的算术平方根是3， $a - b + 2$ 的立方根是2，求 $a - 4 b$ 的平方根．

查看试题解析
23. 如图

(1)、如图，OB是边长为1的正方形的对角线，且OA＝OB，数轴上A点对应的数是：.

(2)、请仿照（1）的做法，在数轴上描出表示 $\sqrt{5}$ 的点.

查看试题解析
24. 如图，长方体的长为15，宽为10，高为20，点B离点C的距离是5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是多少？

查看试题解析
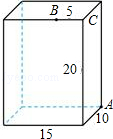25. 已知：如图，把 $△ A B C$ 向上平移3个单位长度，再向右平移2个单位长度，得到 $△ A^{'} B^{'} C^{'}$ .

(1)、写出 $A^{'} ， B^{'} ， C^{'}$ 的坐标；

(2)、点P在y轴上，且 $△ B C P$ 与 $△ A B C$ 的面积相等，求点P的坐标.

查看试题解析
26. 已知x、y为实数，y＝ $\frac{\sqrt{x^{2} - 9} + \sqrt{9 - x^{2}} + 1}{x - 3}$ ，求5x+6y的值.

查看试题解析
27. 一辆汽车油箱内有油48升，从某地出发，每行1km，耗油0.6升，如果设剩油量为y（升），行驶路程为x（千米）.

(1)、写出y与x的关系式；

(2)、这辆汽车行驶35km时，剩油多少升；汽车剩油12升时，行驶了多千米；

(3)、这车辆在中途不加油的情况下最远能行驶多少千米.

查看试题解析
28. 阅读材料，回答问题：
两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，我们就说这两个代数式互为有理化因式.例如：因为 $\sqrt{a} \times \sqrt{a} = a$ ， $(\sqrt{2} + 1) (\sqrt{2} - 1) = 1$ ，所以 $\sqrt{a}$ 与 $\sqrt{a}$ ， $\sqrt{2} + 1$ 与 $\sqrt{2} - 1$ 互为有理化因式.

(1)、 $2 \sqrt{3} - 1$ 的有理化因式是；

(2)、这样，化简一个分母含有二次根式的式子时，采用分子、分母同乘以分母的有理化因式的方法就可以了，例如： $\frac{2}{\sqrt{3}} = \frac{2 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{2 \sqrt{3}}{3}$ ，
$\frac{\sqrt{5} + \sqrt{3}}{\sqrt{5} - \sqrt{3}} = \frac{{(\sqrt{5} + \sqrt{3})}^{2}}{(\sqrt{5} - \sqrt{3}) (\sqrt{5} + \sqrt{3})} = \frac{5 + 2 \sqrt{15} + 3}{5 - 3} = \frac{8 + 2 \sqrt{15}}{2} = 4 + \sqrt{15}$

用上述方法对 $\frac{2 - \sqrt{3}}{2 + \sqrt{3}}$ 进行分母有理化.

(3)、若 $a = \frac{1}{2 + \sqrt{5}}$ ， $b = 2 - \sqrt{5}$ ，判断 $a$ 与 $b$ 的关系并说明理由.

(4)、直接写结果： $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \dots + \frac{1}{\sqrt{2020} + \sqrt{2019}}) (\sqrt{2020} + 1) =$ .

查看试题解析

质量x(千克)	1	2	3	4	5
售价y(元)	2＋0.1	4＋0.2	6＋0.3	8＋0.4	10＋0.5